Artículo satírico en polémica con el problemista portugués Eduardo Valente sobre los "posibles"(??) mensajes o arcanos matemáticos ocultos en el tablero.

Publicado en portugués en la “Enciclopedia Damista”

&&&&&&&&

&&&&

He esperado un tiempo para hacer público un descubrimiento que de seguro va a cambiar la forma de pensar en las Damas e incluso en la propia esencia del juego.

Yo mismo me negaba a creer lo que ahora es evidente para mí pero la fuerza de los extraordinarios hechos ocurridos me lleva a creer lo que me parecía increíble: el juego de Damas en su misma esencia puede ser más que un juego y su estructura final está desarrollada conforme a leyes y reglas que a los humanos se nos escapan, pero quien las trazó lo hizo siguiendo estrictos principios matemáticos de profunda significación y de los que solo podemos entrever pequeños retazos.

Es por ello que estaré siempre en deuda con quien primero me lo mostró (desde ahora “El Maestro”) y con su gran intuición, la cual queda demostrada una vez más en los hechos que siguen.

Recientemente han aparecido en la biblioteca del Real Monasterio de El Escorial de Madrid algunos códices, incunables y otros viejos libros de finales del siglo XV y principios del XVI que desde el primer momento han intrigado a los expertos y están estudiándose con gran entusiasmo.

Uno de estos antiguos documentos ha llamado especialmente la atención de un experto en la época medieval y amigo mío que los está sometiendo a estudio, pues en ellos parece que se reflejan cuestiones sobre el juego de Damas, acompañados de ciertas estructuras geométricas y sonetos con sentido casi religioso. Este amigo, recordando mi afición por tales temas me llamó y juntos hemos seguido estudiando los documentos.

En efecto, un incunable datado posiblemente entre 1495-1500 contenía varias referencias al juego de Damas que desde el principio me sorprendieron; eran tres (3) páginas, que en caso de haber estado numeradas como en la actualidad corresponderían a la 6,7 y 8 del libro.

Este dato no llamó mi atención en el primer momento, pero ahora veo gran significado en él, como posteriormente mostraré. Sí observé que 6+7+8=21=7x3, cuya descomposición en números primos resulta ser nuevamente la referencia al factor “3” junto al número “7”, de gran consideración cabalística desde antiguo y número primo de “Mersenne”. Solo después pude comprobar la enorme importancia de los números 6,7 y 8 en la gran trama del tablero (¿o quizá en algo más profundo?) como mostraré a continuación.

Tres (3) dibujos del damero clásico, uno de ellos con la numeración del juego, otro con tres (3) damas blancas dibujadas en las 3 primeras casas y donde se observaba dibujada una “estrella” compuesta por cuatro triángulos isósceles. El tercer tablero contenía lo que parecía ser un problema.

Además dibujados en las tres páginas aparecían algunos triángulos rectángulos, lo que añadía otro misterio para mí.

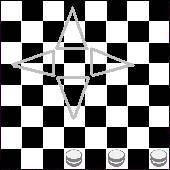
(1) (2)

Como se puede suponer, todo esto me intrigó pero aún más lo hicieron los sonetos al pie de los tableros:

“En estas tablas se encuentra la esencia de todo, el todo es trinitario y oculto al hombre, excepto para los más notables entre ellos que lo podrán entrever y cuyo mayor adalid aquí se anuncia”.

Quedé perplejo; sin duda la “tabla” era el damero, lo “trinitario” se podía referir a la Trinidad cristiana o solo al número 3, que parecía sugerirse también por los triángulos (3 lados, 3 ángulos) y el resto de los indicios, pero no comprendía como todo esto podía anunciar a él o los maestros que nos lo desvelarían.

Durante varios días apenas pude dormir hasta que pensando en los dibujos triangulares encontré la primera pista: la sucesión de los cuatro triángulos isósceles girando 90º cada unos respecto al anterior en uno de los tableros. Esto me llevo a pensar en la posición clave de la forzosa ya que además el dibujo (1) parecía sugerirla ¿y si los triángulos representan las damas en (10,11,22), (18,15,23), (11,22,23) y (10,15,18) propias del triangulo mortal de la forzosa?

Era una idea ¿pero como se une con el resto? De principio me intrigó la situación de las damas en (1), pues las casillas 1,2 y 3 coordinaban de forma total con el resto de la información del incunable, incluso casi de forma cabalística ya que además la suma y el producto de estos tres números es 6, número sabido perfecto desde la antigüedad. Es más, el número 6 es el primer perfecto entre todos los números y además es triangular (¡otra vez el factor 3!), o sea suma de enteros consecutivos.

Pero además posee otra propiedad respecto al factor “3”, esta vez por defecto, ya que increíblemente es el único número perfecto que no es suma parcial ¡de los cubos de números impares consecutivos! Incluso ahora conozco que su factorización 6=2x3, nos refleja dos números que juntos volverán a ser claves en mi investigación.

Nuevamente el factor “3” y lo cúbico por todas partes, ¿cuál seria su significado dentro del juego?¿ o iba más allá del juego?

Entonces una idea cruzó como un relámpago por mi cabeza, corrí hacia mi amigo y le dije: “creo que los antiguos nos quieren comunicar la esencia geométrico-numérica del juego y su posible relación con otros misterios, empezando por cuestiones básicas como los finales”.

Dicho esto una lluvia de ideas pasaron por mi mente, pero ya veía las cosas más claras. La primera información (la rotación “triangular”) nos decía como situar las damas en los vértices de los triángulos para realizar la forzosa. De hecho vuelve a ser notable el que se precisen 3 damas para poder ganar el final más importante y básico del juego, precisamente en un damero con 8 (2³) casillas de lado, ya que en otros dameros esto deja de ser así, precisando 4 damas en todos de orden superior; ya no me cabía duda de que el factor 3 es crucial en el damero clásico.

Es más, por primera vez empezaba a vislumbrarse el porqué son 12 los movimientos necesarios para ganar la forzosa y 12 los peones iniciales por bando, pues la suma de sus cifras también nos remite al factor 3 (1+2=3). ¡Incluso en el juego la equivalencia lógica entre dama y peón es 3! (1 dama=3 peones)

Empezaba a estar claro el porqué este damero, plagado de propiedades matemáticas, y no otro había sido elegido para la creación del juego.

Ahora pasaría a los finales de 3 damas (d.p.) contra dama y peón, pero solo en laterales, ya que los demás se podían reducir a estos por ataques o captura. Otra vez surgió la duda ¿cómo relacionar los triángulos con todo esto? En primer lugar pensé en el único de estos finales que no se puede ganar, con peón negro en 8 y no tardé en darme cuenta de una circunstancia: este final es el único en que no se puede formar un triangulo rectángulo con dicho peón y las damas blancas, ocupando además una de ellas la diagonal principal e impidiendo el avance sin captura del peón. Los rectángulos dibujados en el incunable son sin duda una referencia a esta propiedad.

¿Seria esto posible? En efecto, si peón en 9 entonces (1,9,17,18), si en 17 (9,10,17,25), si 25 (9,10,17,25), si 29 (14,22,29,30), si 30 (23,29,30,31), si 31 (22,30,31,32), si 32 (15,23,31,32), si 24 (15,16,24,32) y si 16 (8,16,23,24), como se muestra para dos de los casos en el siguiente tablero:

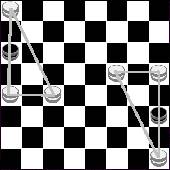
(3)

Todos estos triángulos además se pueden considerar base mortal de estos finales, pues en cualquier lugar la dama contraria se encuentra en red de captura.

¿Pero que sucede con la casilla 8? En efecto, si formamos la configuración (8,14,15,16) no impide el avance del peón sin captura y si formamos (7,8,16,24) además no tenemos la diagonal principal. Por tanto la intuición se confirma y ahora sabemos que la imposibilidad de ganar este final proviene realmente de estructuras geométricas del tablero y más concretamente triangulares.

Parece una excepción el caso de peón en 29, pues puede mover a 25, pero tal caso se resuelve como trivial, ya que deviene en otro ya resuelto bajo las condiciones pedidas.

Las propiedades geométricas del juego ya parecen fuera de toda duda, pero además están indisolublemente ligadas a las propiedades numéricas. Resulta que esta casilla sin solución es la única entre todas las consideradas como base del peón negro cuyo número es un cubo perfecto (8=2³), lo que reincide en lo trinitario señalado ya en los sonetos, así como en las figuras geométricas y propiedades numéricas ya consideradas.

Después consideré el final de 3 damas contra dama y dos peones. Ahora se hace trivial tal estudio si uno de los peones está en 8, pues ya se descarta por el anterior final y se iguala, ¿pero que sucede con los demás casos? Solo después de muchos estudios durante siglos hemos llegado a saber que todos se pueden ganar excepto si los peones se encuentran en 9 y 17, pero ¿los antiguos ya lo sabían y podríamos haberlo deducido fácilmente de haber conocido la verdadera estructura matemática del juego?

En efecto es así y el anterior final igualado nos indica cual será el final superior también igualado. El primer indicio es la misma factorización del número 8=2³, (2 y 3…¡otra vez los mismos que deducimos de 6=2x3, entre otros!) ¿qué sucede si invertimos las cifras de la potencia? ¿su manifiesta importancia puede proporcionarnos más información? Tenemos entonces 3²=9 que es la primera casilla del único final no ganador contra dos peones, pero lo increíble es que la segunda casilla de dicho final ¡es la única que hace posible que la diferencia entre la mayor y la menor sea una potencia cúbica! ¡y además igual a la casilla no ganadora del anterior final! (17-9=8=2³)

En efecto, si el segundo peón se encuentra en 25, entonces 25-9=16 que no es cubo, al igual que las siguientes diferencias con los sucesivos peones a considerar (20,21,22,23,15,7). Por tanto, solo aplicando la numerología del tablero podríamos haber sabido el resultado de estos estudios sin haberlos siquiera realizado ¡increíble la esencia numérica del juego de Damas!

La exactitud de esta regla es tan increíble que incluso si consideramos el caso obvio de segundo peón en 8 y aplicamos la regla de la resta entre casillas, tenemos: 9-8=1=1³, ¡que sí es cubo y nos indica su imposibilidad de resolución! Al día de hoy todavía no salgo de mi asombro.

En el momento actual me encuentro en la deducción numérica del siguiente final (contra tres peones) lo cual representa un paso más en la total deducción geométrico-numérica del juego.

De hecho, ahora sabemos que todos los nuevos finales que tengan peones en 9 y 17 son triviales y no entrarán en el estudio, por tanto el siguiente a considerar será con peones en 9 y 25. Si seguimos ahora la regla de diferencias entre mayor y menores tenemos que 25-9=16. Situando dicho final (9,16,25) y haciendo la diferencia total tenemos que 25-16-9=0, que resulta ser la tercera potencia de sí mismo y por tanto las reglas ya vistas nos dicen que no será posible ganarlo ¡lo que resulta verdadero! Igual sucede si tenemos el peón en 8, pues 25-9-8=8, ¡que sabemos número básico y tercera potencia!

Aturdido por tales descubrimientos fijé la mirada, casi para descansar, sobre el tablero del incunable en que se reflejaba al parecer un problema. En efecto, resultaba ser un problema medianamente complejo pero curioso, que se resuelve con la secuencia 1)7-12,16x7, 2)2-5,9x2, 3)14-19,23x5, 4)30x4 y el negro tiene que entregarse. Ver siguiente tablero con el final de la combinación:

(4)

El descubrimiento del problema era ya muy importante, pues asegura que antes del año 1500 el concepto de problema ya estaba desarrollado, pero algo aún más extraño se reflejaba en esa posición del problema ya resuelto.

Sin poder pensar en otra cosa empecé a escribir los números de las casillas en que estaban situadas las piezas: 1,2,4,5,8,24. ¿qué relación podían tener? Yo estaba seguro que tal relación existía; la primera observación fue que el 24, número mayor, era igual a 3x8, números claves en los secretos numéricos del tablero, al igual que la suma de sus cifras, 2+4=6.

En primer lugar apliqué la regla de las “diferencias mayor-menor”; en este caso seria 24 menos el resto de los números cuya suma es 20 (1+2+4+5+8).

La diferencia es 4 (24-20) y me percaté que este resultado dividía exactamente a la suma de los menores ya que 5x4=20. Además ahora se tiene la terna (5-4-24), que proviene de estas consideraciones e incide en las propiedades “ternarias o trinitarias” del tablero y que curiosamente tiene piezas en tales casillas del tablero. [Ver (4)]

En verdad se pueden formar otras dos ternas(¡total de 3!) con (2-10-24) o (1-20-24), pero se descartan totalmente pues no proceden de consideraciones lógicas como las señaladas para la terna escogida y además no cumplen otras propiedades de esta, ya que a la vista del tablero final (4) se observa que las descomposición (2-10) o (20-1) no tienen ambas piezas en dicho tablero mientras que la (5-4) si las posee.

Es casi inquietante ver como incluso las tres ternas tienen relación directa con el factor 3, pues sumando sus cifras tenemos (1-20)=1+2+0=3, (2-10)=2+1+0=3 y (5-4)=5+4=9=3².

Una vez con (5-4-24), ¿cómo seguir? ¿que nos quieren indicar los antiguos? Un estremecimiento recorrió mi cuerpo cuando después de horas de estudio observé lo siguiente:

Si numeramos el alfabeto español, considerando de forma lógica la letra “A” como ‘1’, “B”=’2’, etc. tenemos:

A(1), B(2), C(3), D(4), E(5), F(6), G(7), H(8), I(9), J(10), K(11), L(12), LL(13), M(14), N(15), Ñ(16), O(17), P(18), Q(19), R(20), S(21), T(22), U(23), V(24), W(25), X(26), Y(27), Z(28).

En ese momento hice la sustitución de la terna de números encontrados (5-4-24) por sus letras respectivas y quedé estupefacto:

E D V

5 4 24

¡Si! ¡Allí estaba el nombre del “Maestro” anunciado en los antiguos sonetos! Ese era el hombre que nos desvelaría el misterio que esconde el tablero y que nos obliga a cambiar radicalmente de pensamiento. Estaba anunciado y los tiempos antiguos nos desvelan su nombre: Eduardo Valente es el “Maestro” profetizado!

La trama del destino es tan oculta y los misterios del tablero tan insondables que nuestras mentes apenas son capaces de darse cuenta que todo esta previsto y medido de forma perfecta. De inmediato me percaté que nombre y apellido de el “Maestro” tienen siete letras cada uno, sumando por tanto 14.

Sustituí todas las letras del nombre y apellido por sus equivalentes alfabéticos e hice la suma, que resulta igual a 158, que no de forma casual ¡también sus cifras suman 14=1+5+8!

Pero el misterio cúbico de los antiguos está enraizado mucho más profundamente aún, pues si sumamos estos dos resultados procedentes del “Maestro” tenemos 14+14=28, ¡que es el siguiente numero perfecto y triangular después del 6!

No contentos con tal profecía, los antiguos aún nos legaron otra muestra más de su total dominio del tablero y del destino, encerrando todo en su concepto cúbico del universo y prediciendo todo a partir de él, pues…¡el número del “Maestro” es igual a la suma de dos potencias cúbicas impares consecutivas! (28=1³+3³).

Ante esta gran revelación, que ahora se hace evidente a mis sentidos, no puedo nada más que decir que “El Maestro” será mi guía a partir de ahora y que solo sus revelaciones y genial intuición alumbrarán mi camino. Él me ha hecho ver la luz.

Anexos:

El problema reflejado en tablero (2) es original del damista cubano Manuel Soriano Felipe y publicado en Enciclopedia Damista(ED) de septiembre de 2003, con nº 5.204. Realmente se puede tomar cualquier tablero y sacar las conclusiones que se deseen.

En referencia a este problema y como respuesta al ensayo de ED con el movimiento 24-28, decir que se hacen tablas inmediatas con 1)24-28, 9-18, 2)14x21,15-11, 3)7x14, 27-31, 4)30x20, 31x25 o26, tablas.

Siguen algunas definiciones de conceptos usados en el artículo:

Número primo: solo divisible de forma entera entre el mismo y la unidad.

Primo de Mersenne: cumple (2^p-1), siendo “p” un primo. P.e: 7=2³-1

Número perfecto: suma de sus divisores excluido el mismo. P.e: 6=1+2+3

Número triangular: suma de enteros consecutivos. P.e: 6 o 28=1+2+3+4+5+6+7.

*************

-Artículo publicado en la Enciclopedia Damista portuguesa en su número de Julio de 2004.

*************

José Luis González Sanz

Todos los derechos reservados

&&&&&&&&&

&&&&&&

&&&

&