LOS 10 MEJORES ALGORITMOS DE CLASIFICACIÓN Y BÚSQUEDA

1.- Búsqueda binaria

2.- Buscar un elemento en una matriz ordenada y rotada

3.- Búsqueda de burbuja

4.- Inserción

5.- Fusión

6.- Montón binario

7.- Quick sort

8.- Búsqueda de interpolación

9.- Encontrar el más pequeño/grande en un conjunto sin clasificar

10.- Dada una matriz ordenada y un número x, encuentra el par en la matriz cuya suma es más cercana a x

&&&&&&&&&&

&&&&&&&

&&&

&

1.- BÚSQUEDA BINARIA

Dada una matriz ordenada arr[] de “n” elementos, escribe una función para buscar un elemento dado “x” en arr[].

Un enfoque sencillo es hacer una búsqueda lineal. La complejidad temporal del algoritmo anterior es O(n). Otro enfoque para realizar la misma tarea es utilizar la búsqueda binaria.

Búsqueda binaria: Buscar una matriz ordenada dividiendo repetidamente el intervalo de búsqueda por la mitad. Comience con un intervalo que cubra toda la matriz. Si el valor de la clave de búsqueda es menor que el elemento en la mitad del intervalo, reduzca el intervalo a la mitad inferior. En caso contrario, acorte el intervalo a la mitad superior. Compruebe repetidamente hasta que se encuentre el valor o el intervalo esté vacío.

Ejemplo:

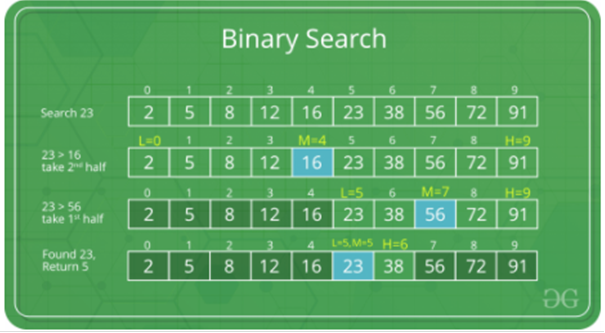
La idea de la búsqueda binaria es utilizar la información que la matriz está ordenada y reducir la complejidad del tiempo a O(Log n).

Básicamente ignoramos la mitad de los elementos sólo después de una comparación.

1.- Compara x con el elemento medio.

2.- Si x coincide con el elemento medio, devolvemos el índice medio.

3.- Si x es mayor que el elemento medio, entonces x sólo puede estar en la mitad derecha de la subred después del elemento medio. Así que recurrimos a la mitad derecha.

4.- Si no (x es más pequeña), recurrimos a la mitad izquierda.

Implementación recursiva de la búsqueda binaria, en lenguaje C++:

#include <bits/stdc++.h>

using namespace std;

// Una función de búsqueda binaria recursiva. Devuelve

// la ubicación de “x” en la matriz dada arr[l.r] si está presente,

//de lo contrario -1

int binarySearch(int arr[], int l, int r, int x)

{

if (r >= l) { int mid = l + (r - l) / 2;

// Si el elemento está presente en el centro mismo

if (arr[mid] == x)  return mid;

// Si el elemento es más pequeño que el medio, entonces sólo puede estar presente en el  subconjunto //izquierdo

if (arr[mid] > x)   return binarySearch(arr, l, mid - 1, x);

// De lo contrario, el elemento sólo puede estar presente en el subconjunto derecho...

return binarySearch(arr, mid + 1, r, x);

}

// Llegamos aquí cuando el elemento no está presente en la matriz

return -1;

}

int main(void)

{

int arr[] = { 2, 3, 4, 10, 40 };

int x = 10;

int n = sizeof(arr) / sizeof(arr[0]);

int result = binarySearch(arr, 0, n - 1, x);

(result == -1) ? cout << "El elemento no se encuentra en la matriz"

: cout << "El elemento está presente en el lugar " << result;

return 0;

}

Salida : El elemento está presente en el lugar 3

Implementación iterativa de la búsqueda binaria, en lenguaje C++:

#include <bits/stdc++.h>

using namespace std;

// Una función de búsqueda binaria iterativa. Devuelve

// la ubicación de “x” en la matriz dada arr[l.r] si está presente,

//de lo contrario -1

int binarySearch(int arr[], int l, int r, int x)

{

while (l <= r) { int m = l + (r - l) / 2;

// Comprueba si está presente en el centro

if (arr[m] == x)  return m;

// Si es mayor, busca en la parte izquierda

if (arr[m] < x)    l = m + 1;

// Si “x” es más pequeño, ignora la mitad derecha

else  r = m - 1;

}

// Llegamos aquí cuando el elemento no está presente en la matriz   

return -1;

}

int main(void)

{

int arr[] = { 2, 3, 4, 10, 40 };

int x = 10;

int n = sizeof(arr) / sizeof(arr[0]);

int result = binarySearch(arr, 0, n - 1, x);

(result == -1) ? cout << " El elemento no se encuentra en la matriz "

: cout << " El elemento está presente en el lugar " << result;

return 0;

}

Salida : El elemento está presente en el lugar 3

La complejidad temporal de la Búsqueda Binaria puede escribirse como    T(n) = T(n/2) + c

2.- Buscar un elemento en una matriz ordenada y rotada

Un elemento de una matriz ordenada se puede encontrar en tiempo O(log n) por medio de una búsqueda binaria.

Pero supongamos que rotamos una matriz ordenada en orden ascendente en algún pivote desconocido de antemano. Así, por ejemplo, 1 2 3 4 5 podría convertirse en 3 4 5 1 2. Idear una manera de encontrar un elemento en la matriz rotada en O(log n) tiempo. 

Ejemplos:

Entrada: arr[]={5,6,7,8,9,10,1,2,3} pivote=3 Salida= 8

Básicamente:

La idea es encontrar el punto de giro, dividir la matriz en dos submatrices y realizar una búsqueda binaria.

La idea principal para encontrar el punto de giro es - para una matriz ordenada (en orden creciente) y pivotada, el elemento de giro es el único elemento para el cual el siguiente elemento a él es más pequeño que él.

Utilizando la afirmación anterior y la búsqueda binaria se puede encontrar el pivote.

Después de encontrar el pivote, dividir la matriz en dos submatrices.

Ahora las submatrices individuales se ordenan para que el elemento pueda ser buscado usando la búsqueda binaria.

Implementación:

Entrada arr[] = {3, 4, 5, 1, 2}

Elemento a buscar = 1

1) Averiguar el punto de pivote y dividir la matriz en dos

submatrices. (pivote = 2) /*Índice de 5*/

2) Ahora llama a la búsqueda binaria de uno de los dos submatrices.

a) Si el elemento es mayor que el 0º elemento entonces

buscar en la matriz izquierda

b) Otra búsqueda en la matriz derecha

(1 irá en otro como 1 < 0 elemento(3))

3) Si el elemento se encuentra en un subconjunto seleccionado, entonces el índice de retorno

Si no, regresa -1.

A continuación se muestra la aplicación del enfoque anterior en lenguaje C++: 

#include <bits/stdc++.h>

using namespace std;

int binarySearch(int arr[], int low, int high, int key)

{

if (high < low) return -1;

int mid = (low + high) / 2; /*low + (high - low)/2;*/

if (key == arr[mid])   return mid;

if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key);

    // else

return binarySearch(arr, low, (mid - 1), key);

}

/* Toma pivote de la matriz 3, 4, 5, 6, 1, 2

   retorna 3 (indice de 6) */

int findPivot(int arr[], int low, int high)

{

if (high < low)     return -1;

if (high == low)   return low;

int mid = (low + high) / 2; /*low + (high - low)/2;*/

if (mid < high && arr[mid] > arr[mid + 1])  return mid;

if (mid > low && arr[mid] < arr[mid - 1])  return (mid - 1);

if (arr[low] >= arr[mid]) return findPivot(arr, low, mid - 1);

return findPivot(arr, mid + 1, high);

}

int pivotedBinarySearch(int arr[], int n, int key)

{

int pivot = findPivot(arr, 0, n - 1);

if (pivot == -1)  return binarySearch(arr, 0, n - 1, key);

if (arr[pivot] == key)  return pivot;

if (arr[0] <= key) return binarySearch(arr, 0, pivot - 1, key);

return binarySearch(arr, pivot + 1, n - 1, key);

}

/* Programa principal */

int main()

{

int arr1[] = { 5, 6, 7, 8, 9, 10, 1, 2, 3 };

int n = sizeof(arr1) / sizeof(arr1[0]);

int key = 3;

    // Funcion de llamada

cout << "El índice del elemento es : "

         << pivotedBinarySearch(arr1, n, key);

return 0;

}

Salida: el índice del elemento es 8

Complejidad del análisis: Tiempo en O(log n)

3.- Búsqueda de burbuja

La búsqueda de burbuja es el algoritmo de clasificación más simple que funciona intercambiando repetidamente los elementos adyacentes si están en un orden incorrecto.

Por ejemplo:

-Primer paso:

( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Aquí, el algoritmo compara los dos primeros elementos, e intercambia 5 y 1

( 1 5 4 2 8 ) –>  ( 1 4 5 2 8 ), Intercambia 5 y 4
( 1 4 5 2 8 ) –>  ( 1 4 2 5 8 ), Intercambia 5 y 2
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Ahora bien, como estos elementos ya están en orden (8 > 5), el algoritmo no los intercambia

-Segundo paso:

( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Intercambia 4 y 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –>  ( 1 2 4 5 8 )

Ahora, la matriz ya está ordenada, pero nuestro algoritmo no sabe si está completa. El algoritmo necesita una pasada completa sin ningún intercambio para saber que está ordenado.

-Tercer paso:

( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

Ahora, al no haber realizado ningún intercambio, el algoritmo se ha “convencido” de que la matriz está ordenada. Seguidamente el código en lenguaje C++:

#include <bits/stdc++.h>

using namespace std;

void swap(int *xp, int *yp) 

{ 

int temp = *xp; 

    *xp = *yp; 

    *yp = temp; 

} 

void bubbleSort(int arr[], int n) 

{ 

int i, j; 

for (i = 0; i < n-1; i++)     

for (j = 0; j < n-i-1; j++) 

if (arr[j] > arr[j+1]) 

            swap(&arr[j], &arr[j+1]); 

} 

/* Imprime resultados */

void printArray(int arr[], int size) 

{ 

int i; 

for (i = 0; i < size; i++) 

cout << arr[i] << " "; 

cout << endl; 

} 

// Programa principal 

int main() 

{ 

int arr[] = {64, 34, 25, 12, 22, 11, 90}; 

int n = sizeof(arr)/sizeof(arr[0]); 

bubbleSort(arr, n); 

cout<<"Sorted array: \n"; 

printArray(arr, n); 

return 0; 

} 

Salida: 11,12,22,25,34,64,90

La función anterior siempre se ejecuta en tiempo O(n^2) incluso si la matriz está ordenada. Puede ser optimizada deteniendo el algoritmo si el bucle interno no causó ningún intercambio.

4.- INSERCIÓN

La clasificación por inserción es un simple algoritmo de clasificación que funciona de manera similar a la forma en que se clasifican las cartas en las manos. La matriz se divide virtualmente en una parte clasificada y otra no clasificada. Los valores de la parte sin clasificar se escogen y se colocan en la posición correcta en la parte clasificada.

Algoritmo:

Para clasificar un conjunto de tamaño n en orden ascendente:

1: Iterar del arr[1] al arr[n] sobre la matriz.

2: Comparar el elemento actual (clave) con su predecesor.

3: Si el elemento clave es más pequeño que su predecesor, compáralo con los elementos anteriores. Mueva los elementos mayores una posición hacia arriba para hacer espacio para el elemento intercambiado.

Ejemplo:

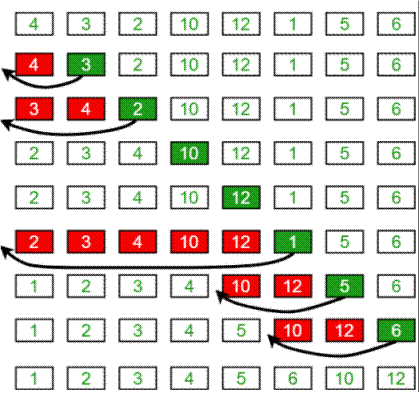
En lenguaje C++:

#include <bits/stdc++.h>

using namespace std;

void insertionSort(int arr[], int n) 

{ 

int i, key, j; 

for (i = 1; i < n; i++)

    { 

key = arr[i]; 

        j = i - 1; 

while (j >= 0 && arr[j] > key)

        { 

arr[j + 1] = arr[j]; 

            j = j - 1; 

        } 

arr[j + 1] = key; 

    } 

} 

//Imprime resultado

void printArray(int arr[], int n) 

{ 

int i; 

for (i = 0; i < n; i++) 

cout << arr[i] << " "; 

cout << endl;

} 

//Programa principal

int main() 

{ 

int arr[] = { 12, 11, 13, 5, 6 }; 

int n = sizeof(arr) / sizeof(arr[0]); 

insertionSort(arr, n); 

printArray(arr, n); 

return 0; 

} 

Salida: 5,6,11,12,13

Complejidad del tiempo: O(n*2) Espacio auxiliar: O(1)

Casos límite: La clasificación de inserción toma el máximo tiempo para clasificar si los elementos se clasifican en orden inverso. Y toma el mínimo tiempo (Orden de n) cuando los elementos ya están ordenados.

Paradigma algorítmico: Enfoque incremental

Usos: El tipo de inserción se utiliza cuando el número de elementos es pequeño. También puede ser útil cuando la matriz de entrada está casi ordenada, sólo unos pocos elementos se pierden en la gran matriz completa.

¿Qué es la clasificación de inserción binaria?

Podemos usar la búsqueda binaria para reducir el número de comparaciones en la clasificación de inserción normal. El Ordenador de Inserción Binario utiliza la búsqueda binaria para encontrar la ubicación adecuada para insertar el elemento seleccionado en cada iteración. En la inserción normal, la clasificación toma O(i) (en la iteración ith) en el peor de los casos. Podemos reducirlo a O(logi) utilizando la búsqueda binaria. El algoritmo, en su conjunto, sigue teniendo un tiempo de ejecución en el peor de los casos de O(n2) debido a la serie de intercambios necesarios para cada inserción.

5.- FUSIÓN

Al igual que Inserción, Fusión es un algoritmo de divide y vencerás. Divide la matriz de entrada en dos mitades, se llama a sí mismo para las dos mitades y luego fusiona las dos mitades ordenadas. La función merge() se usa para fusionar dos mitades. La función merge(arr, l, m, r) es un proceso clave que asume que arr[l..m] y arr[m+1..r] están ordenados y fusiona los dos subconjuntos ordenados en uno. Véase la siguiente implementación de C para más detalles.

MergeSort(arr[], l, r)

Si r > l

1. Encuentra el punto medio para dividir la matriz en dos mitades:

m medio = (l+r)/2

2. Llama a MergeSort para la primera mitad:

Llama a fusionarSorprender(arr, l, m)

3. Llama a MergeSort para el segundo tiempo:

Llama a fusionarOrdenar(arr, m+1, r)

4. Fusiona las dos mitades clasificadas en los pasos 2 y 3:

Llama a fusionar (arr, l, m, r)

El siguiente diagrama de wikipedia muestra el proceso completo de clasificación de fusión para un ejemplo de matriz {38, 27, 43, 3, 9, 82, 10}. Si miramos más de cerca el diagrama, podemos ver que la matriz se divide recursivamente en dos mitades hasta que el tamaño se convierte en 1. Una vez que el tamaño se convierte en 1, los procesos de fusión entran en acción y comienzan a fusionar matrices hasta que la matriz completa se fusiona.

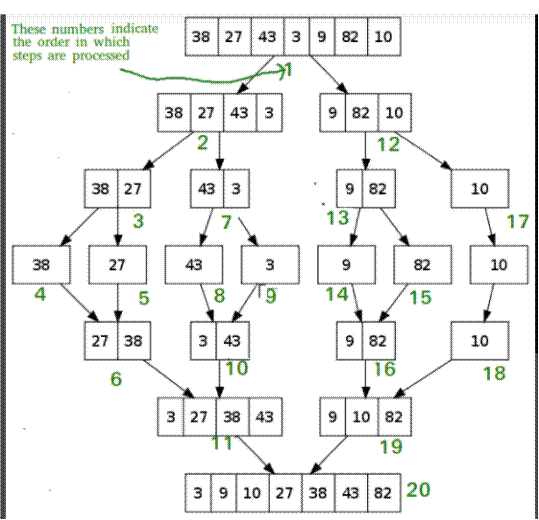
En lenguaje C++:

#include <stdio.h>

#include <stdlib.h>

void merge(int arr[], int l, int m, int r)

{

int i, j, k;

int n1 = m - l + 1;

int n2 = r - m;

int L[n1], R[n2];

for (i = 0; i < n1; i++)         L[i] = arr[l + i];

for (j = 0; j < n2; j++)         R[j] = arr[m + 1 + j];

     i = 0;   j = 0;  k = l;

while (i < n1 && j < n2) {

if (L[i] <= R[j]) {

arr[k] = L[i];

            i++;

        }

else {

arr[k] = R[j];

j++;

        }

        k++;

    }

while (i < n1) {

arr[k] = L[i];

        i++;

        k++;

    }

while (j < n2) {

arr[k] = R[j];

j++;

        k++;

    }

}

void mergeSort(int arr[], int l, int r)

{

if (l < r) {

int m = l + (r - l) / 2;

mergeSort(arr, l, m);

mergeSort(arr, m + 1, r);

merge(arr, l, m, r);

    }

}

void printArray(int A[], int size)

{

int i;

for (i = 0; i < size; i++)

printf("%d ", A[i]);

printf("\n");

}

//Programa principal

int main()

{

int arr[] = { 12, 11, 13, 5, 6, 7 };

int arr_size = sizeof(arr) / sizeof(arr[0]);

printf("Given array is \n");

printArray(arr, arr_size);

mergeSort(arr, 0, arr_size - 1);

printf("\nSorted array is \n");

printArray(arr, arr_size);

return 0;

}

Salida: 5,6,7,11,12,13

Complejidad del tiempo: Clasificando conjuntos en diferentes máquinas. Fusión es un algoritmo recursivo y la complejidad temporal puede expresarse como la siguiente relación de recurrencia.

T(n) = 2T(n/2) + Ɵ(n)

La recurrencia anterior puede resolverse mediante el método del Árbol de Recurrencia o el método Maestro. Cae en el caso II del método Maestro y la solución de la recurrencia es Ɵ(nLogn).

La complejidad temporal de Fusión es Ɵ(nLogn) en los 3 casos (peor, promedio y mejor) ya que Fusión siempre divide la matriz en dos mitades y toma un tiempo lineal para fusionar dos mitades.

6.- montón binario

La clasificación en pila es una técnica de clasificación basada en la comparación de la estructura de datos de la pila binaria. Es similar a la clasificación de selección donde primero encontramos el máximo elemento y colocamos el máximo elemento al final. Repetimos el mismo proceso para los elementos restantes.

Primero definamos un Árbol Binario Completo. Un árbol binario completo es un árbol binario en el que cada nivel, excepto posiblemente el último, está completamente lleno, y todos los nodos están lo más a la izquierda posible (Fuente Wikipedia)

Un Montón Binario es un Árbol Binario Completo en el que los elementos se almacenan en un orden especial tal que el valor en un nodo padre es mayor (o menor) que los valores en sus dos nodos hijos. El primero se denomina max heap y el segundo min-heap. El heap puede representarse mediante un árbol o matriz binaria.

¿Por qué la representación basada en un array para el Binary Heap?

Dado que un Montón Binario es un Árbol Binario Completo, puede ser fácilmente representado como un array y la representación basada en el array es eficiente en cuanto a espacio. Si el nodo padre está almacenado en el índice I, el hijo izquierdo puede ser calculado por 2 * I + 1 y el hijo derecho por 2 * I + 2 (asumiendo que la indexación comienza en 0).

Algoritmo de clasificación en pila para clasificar en orden creciente:

1. Construye un montón máximo a partir de los datos de entrada.

2. En este punto, el elemento más grande se almacena en la raíz del montón. Reemplazarlo por el último elemento del montón seguido de reducir el tamaño del montón en 1. Finalmente, amontonar la raíz del árbol.

3. Repita el paso 2 mientras el tamaño del montón sea mayor que 1.

¿Cómo construir el montón?

El procedimiento de apilamiento puede aplicarse a un nodo sólo si sus nodos hijos están apilados. Por lo tanto, la amontonamiento debe realizarse en el orden de abajo hacia arriba.

Entendamos con la ayuda de un ejemplo:

Entrada: 4, 10, 3, 5, 1

4(0)

/ \

10(1) 3(2)

/ \

5(3) 1(4)

Los números entre paréntesis representan los índices de la matriz

representación de los datos.

Aplicando el procedimiento de heapify al índice 1:

4(0)

/ \

10(1) 3(2)

/ \

5(3) 1(4)

Aplicando al índice 0:

10(0)

/ \

5(1) 3(2)

/ \

4(3) 1(4)

En lenguaje C++:

#include <iostream>   

using namespace std;

void heapify(int arr[], int n, int i)

{

int largest = i;

int l = 2*i + 1;

int r = 2*i + 2;  

if (l < n && arr[l] > arr[largest])

largest = l;   

if (r < n && arr[r] > arr[largest])

largest = r;

if (largest != i)

    {

        swap(arr[i], arr[largest]);   

heapify(arr, n, largest);

    }

}

void heapSort(int arr[], int n)

{

for (int i = n / 2 - 1; i >= 0; i--)   heapify(arr, n, i);

for (int i=n-1; i>0; i--)

    {

        swap(arr[0], arr[i]);  

heapify(arr, i, 0);

    }

}

void printArray(int arr[], int n)

{

for (int i=0; i<n; ++i)

cout << arr[i] << " ";

cout << "\n";

}

// Programa principal

int main()

{

int arr[] = {12, 11, 13, 5, 6, 7};

int n = sizeof(arr)/sizeof(arr[0]);   

heapSort(arr, n);   

cout << "Sorted array is \n";

printArray(arr, n);

}

Salida: 5,6,7,11,12,13

Complejidad: La complejidad temporal de la pila es O(Logn). La complejidad temporal de createAndBuildHeap() es O(n) y la complejidad temporal general de Heap Sort es O(nLogn).

7.- Quick sort

Al igual que Fusión, QuickSort es un algoritmo de Divide y Vencerás. Escoge un elemento como pivote y divide la matriz dada alrededor del pivote escogido. Hay muchas versiones diferentes de quickSort que escogen el pivote de diferentes maneras.

Siempre escoge el primer elemento como pivote.

Siempre elige el último elemento como pivote (implementado abajo)

Escoge un elemento aleatorio como pivote.

Escoge la mediana como pivote.

El proceso clave en quickSort es partition(). El objetivo de las particiones es, dada una matriz y un elemento x de la matriz como pivote, poner x en su posición correcta en la matriz ordenada y poner todos los elementos más pequeños (más pequeños que x) antes de x, y poner todos los elementos más grandes (más grandes que x) después de x. Todo esto debe hacerse en tiempo lineal.

Pseudocódigo de la función recursiva:

/* low --> Índice inicial, high --> Índice final */

quickSort(arr[], bajo, alto)

{

si (bajo < alto)

{

/* pi está partiendo el índice, arr[pi] es ahora

en el lugar correcto */

pi = partición(arr, bajo, alto);

quickSort(arr, low, pi - 1); // Antes de pi

quickSort(arr, pi + 1, alto); // Después de pi

}

}

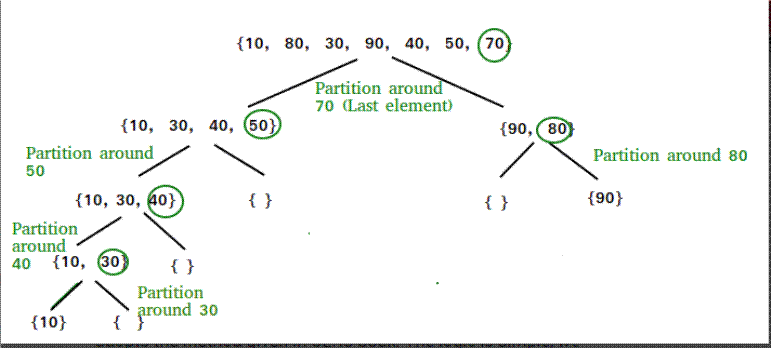
En lenguaje C++:

#include <bits/stdc++.h>

using namespace std; 

void swap(int* a, int* b) 

{ 

int t = *a; 

    *a = *b; 

    *b = t; 

} 

int partition (int arr[], int low, int high) 

{ 

int pivot = arr[high];

int i = (low - 1);

for (int j = low; j <= high - 1; j++) 

    { 

if (arr[j] < pivot) 

        { 

            i++; // increment index of smaller element

            swap(&arr[i], &arr[j]); 

        } 

    } 

    swap(&arr[i + 1], &arr[high]); 

return (i + 1); 

} 

void quickSort(int arr[], int low, int high) 

{ 

if (low < high) 

    { 

int pi = partition(arr, low, high); 

quickSort(arr, low, pi - 1); 

quickSort(arr, pi + 1, high); 

    } 

} 

void printArray(int arr[], int size) 

{ 

int i; 

for (i = 0; i < size; i++) 

cout << arr[i] << " "; 

cout << endl; 

} 

// Programa principal

int main() 

{ 

int arr[] = {10, 7, 8, 9, 1, 5}; 

int n = sizeof(arr) / sizeof(arr[0]); 

quickSort(arr, 0, n - 1); 

cout << "Sorted array: \n"; 

printArray(arr, n); 

return 0; 

} 

Salida:1,5,7,8,9,10

Análisis de QuickSort:

El tiempo que toma la QuickSort en general puede escribirse como sigue.

T(n) = T(k) + T(n-k-1) + Ɵ(n)

Los dos primeros términos son para dos llamadas recursivas, el último término es para el proceso de partición. k es el número de elementos que son más pequeños que el pivote.

El tiempo que tarda QuickSort depende de la matriz de entrada y la estrategia de partición.

8.- Búsqueda de interpolación

Dada una matriz ordenada de n valores uniformemente distribuidos arr[], escribe una función para buscar un elemento particular x en la matriz.

La Búsqueda Lineal encuentra el elemento en O(n) tiempo, la Búsqueda por Salto toma O(√ n) tiempo y la Búsqueda Binaria toma O(Log n) tiempo.

La Búsqueda por Interpolación es una mejora con respecto a la Búsqueda Binaria para los casos en que los valores de una matriz ordenada están distribuidos uniformemente. La Búsqueda Binaria siempre va al elemento medio para comprobar. Por otro lado, la búsqueda de interpolación puede ir a diferentes lugares según el valor de la clave que se busca. Por ejemplo, si el valor de la clave está más cerca del último elemento, es probable que la búsqueda de interpolación comience la búsqueda hacia el lado final.

Para encontrar la posición a buscar, se utiliza la siguiente fórmula.

// La idea de la fórmula es devolver un valor más alto

// cuando el elemento a buscar está más cerca de arr[h]ablar. Y

// menor valor cuando se acerca a arr[lo]

pos = lo + [ (x-arr[lo])*(hi-lo) / (arr[hi]-arr[Lo]) ]

arr[] ==> Matriz donde los elementos deben ser buscados

x ==> Elemento a buscar

lo ==> Índice de partida en arr[]

hi ==> Índice de terminación en arr[]

Algoritmo:

El resto del algoritmo de interpolación es el mismo, excepto la lógica de partición anterior.

Paso 1: En un bucle, calcula el valor de "pos" usando la fórmula de la posición de la sonda.

Paso2: Si coincide, devuelva el índice del elemento y salga.

Paso3: Si el elemento es menor que arr[pos], calcule la posición de la sonda de la submatriz izquierda. De lo contrario, calcule la misma en la submatriz derecha.

Paso4: Repita hasta encontrar una coincidencia o hasta que el subconjunto se reduzca a cero.

En lenguaje C++:

#include<bits/stdc++.h>

using namespace std;

int interpolationSearch(int arr[], int n, int x)

{

int lo = 0, hi = (n - 1);

while (lo <= hi && x >= arr[lo] && x <= arr[hi])

    {

if (lo == hi)

        {

if (arr[lo] == x) return lo;

return -1;

        }

int pos = lo + (((double)(hi - lo) /

            (arr[hi] - arr[lo])) * (x - arr[lo]));

if (arr[pos] == x)    return pos;

if (arr[pos] < x)    lo = pos + 1;

else

            hi = pos - 1;

    }

return -1;

}

// Programa principal

int main()

{

int arr[] = {10, 12, 13, 16, 18, 19, 20, 21,

                 22, 23, 24, 33, 35, 42, 47};

int n = sizeof(arr)/sizeof(arr[0]);

int x = 18;

int index = interpolationSearch(arr, n, x);

if (index != -1)

cout << "Element found at index " << index;

else

cout << "Element not found.";

return 0;

}

El elemento encontrado tiene el índice 4

Complejidad temporal: Si los elementos están distribuidos uniformemente, entonces O (log log n)). En el peor de los casos puede llevar hasta O(n).

Espacio auxiliar: O(1)

9.- Encontrar el más pequeño/grande en un conjunto sin clasificar

Dada una matriz y un número k donde k es más pequeño que el tamaño de la matriz, necesitamos encontrar el elemento más pequeño en la matriz dada. Se da que todos los elementos de la matriz son distintos

Ejemplo:

Entrada: arr[] = {7, 10, 4, 3, 20, 15}

k = 3 Salida: 7

#include<iostream>

#include<climits>

#include<cstdlib>

using namespace std;

int randomPartition(int arr[], int l, int r);

int kthSmallest(int arr[], int l, int r, int k)

{

if (k > 0 && k <= r - l + 1)

    {

int pos = randomPartition(arr, l, r);

if (pos-l == k-1)    return arr[pos];

if (pos-l > k-1)      return kthSmallest(arr, l, pos-1, k);

return kthSmallest(arr, pos+1, r, k-pos+l-1);

    }

return INT_MAX;

}

void swap(int *a, int *b)

{

int temp = *a;

    *a = *b;

    *b = temp;

}

int partition(int arr[], int l, int r)

{

int x = arr[r], i = l;

for (int j = l; j <= r - 1; j++)

    {

if (arr[j] <= x)

        {

            swap(&arr[i], &arr[j]);

            i++;

        }

    }

    swap(&arr[i], &arr[r]);

return i;

}

int randomPartition(int arr[], int l, int r)

{

int n = r-l+1;

int pivot = rand() % n;

    swap(&arr[l + pivot], &arr[r]);

return partition(arr, l, r);

}

//Programa principal

int main()

{

int arr[] = {12, 3, 5, 7, 4, 19, 26};

int n = sizeof(arr)/sizeof(arr[0]), k = 3;

cout << "K'th smallest element is " << kthSmallest(arr, 0, n-1, k);

return 0;

}

Salida: 5

Complejidad: La complejidad temporal del peor caso de la solución anterior sigue siendo O(n2). En el peor de los casos, la función aleatoria siempre puede elegir un elemento de esquina. La complejidad temporal esperada de la QuickSelect aleatoria anterior es O(n). La suposición del análisis es que el generador de números aleatorios tiene la misma probabilidad de generar cualquier número en el rango de entrada.

10.- Dada una matriz ordenada y un número x, encuentra el par en la matriz cuya suma es más cercana a x

Dada una matriz ordenada y un número x, encuentra un par en la matriz cuya suma sea más cercana a x.

Ejemplos:

Entrada: arr[] = {10, 22, 28, 29, 30, 40}, x = 54

Salida: 22 y 30

Entrada: arr[] = {1, 3, 4, 7, 10}, x = 15

Salida: 4 y 10

Una solución sencilla es considerar cada par y hacer un seguimiento del par más cercano (la diferencia absoluta entre la suma del par y x es mínima). Finalmente imprime el par más cercano. La complejidad temporal de esta solución es O(n2)

Una solución eficiente puede encontrar el par en O(n) tiempo. La idea es similar al método 2 de este post. A continuación se detalla el algoritmo.

1) Inicializar una variable diff como infinita (Diff se utiliza para almacenar el

diferencia entre el par y la x). Necesitamos encontrar la mínima diferencia.

2) Inicializar dos variables de índice l y r en la matriz ordenada dada.

a) Inicializar primero al índice más a la izquierda: l = 0

b) Iniciar en segundo lugar el índice más a la derecha: r = n-1

3) Lazo mientras l < r.

a) Si abs(arr[l] + arr[r] - suma) < diff entonces

actualizar diff y resultado

b) Si (arr[l] + arr[r] < suma ) entonces l++

(c) Si no...

A continuación se muestra la implementación del algoritmo anterior.

#include <bits/stdc++.h>

using namespace std;

void printClosest(int arr[], int n, int x)

{

int res_l, res_r;   

int l = 0, r = n-1, diff = INT_MAX;

while (r > l)

    {

if (abs(arr[l] + arr[r] - x) < diff)

       {

res_l = l;

res_r = r;

diff = abs(arr[l] + arr[r] - x);

       }

if (arr[l] + arr[r] > x)

           r--;

else

           l++;

    }

cout <<" El par más cercano es " << arr[res_l] << " y " << arr[res_r];

}

// Programa principal

int main()

{

int arr[] =  {10, 22, 28, 29, 30, 40}, x = 54;

int n = sizeof(arr)/sizeof(arr[0]);

printClosest(arr, n, x);

return 0;

}

Salida: El par más cercano es 22 y 30

&&&&&&&&&&&&&&&&

&&&&&&&&&&&

&&&&&&

&&&

&