

LOS
10 MEJORES ALGORITMOS DE PROGRAMACIÓN DINÁMICA
&&&&&&&&&&
&&&&&&&
&&&
&
1.-
Más larga subsecuencia común
Hemos
discutido los sub-problemas superpuestos y las propiedades de la subestructura
óptima en el Set 1 y el Set 2 respectivamente. También hemos discutido un
problema de ejemplo en el Conjunto 3. Discutamos el problema de la Más Larga Subsecuencia Común (LCS) como un problema de ejemplo más
que puede ser resuelto usando la Programación Dinámica.
Declaración
del problema LCS: Dadas dos secuencias, encontrar la duración de la más larga subsecuencia presente en ambas. Una subsecuencia
es una secuencia que aparece en el mismo orden relativo, pero no necesariamente
contigua. Por ejemplo, "abc", "abg", "bdf",
"aeg", '"acefg",
.. etc. son subsecuencias de "abcdefg".
Para
averiguar la complejidad del enfoque de la fuerza bruta, es necesario conocer
primero el número de posibles subsiguientes diferentes de una cuerda con
longitud n, es decir, encontrar el número de subsiguientes con longitudes que
oscilan entre 1,2,..n-1. Recordemos de la teoría de la permutación y
combinación que el número de combinaciones con 1 elemento son nC1. El número de
combinaciones con 2 elementos son nC2 y así sucesivamente. Sabemos que nC0 +
nC1 + nC2 + ... nCn = 2n. Por lo tanto, una cadena de
longitud n tiene 2n-1 posibles subsiguientes diferentes ya que no consideramos
la subsiguiente con longitud 0. Esto implica que la complejidad temporal del
enfoque de la fuerza bruta será O(n * 2n). Obsérvese que lleva O(n) tiempo
comprobar si una subsecuencia es común a ambas
cadenas. Esta complejidad temporal puede mejorarse utilizando una programación
dinámica.
Es
un problema clásico de la informática, la base de diff
(un programa de comparación de archivos que produce las diferencias entre dos
archivos), y tiene aplicaciones en la bioinformática.
Ejemplos:
Para
las secuencias de entrada "ABCDGH" y "AEDFHR" es
"ADH" de longitud 3.
Para
las secuencias de entrada "AGGTAB" y "GXTXAYB" es
"GTAB" de longitud 4.
La
solución sencilla para este problema es generar todas las subsecuencias
de ambas secuencias dadas y encontrar la subsecuencia
coincidente más larga. Esta solución es exponencial en términos de complejidad
temporal. Veamos cómo este problema posee las dos importantes propiedades de un
problema de programación dinámica (DP).
1)
Subestructura óptima:
Que
las secuencias de entrada sean X[0..m-1] e Y[0..n-1] de longitudes m y n
respectivamente. Y que L(X[0..m-1], Y[0..n-1]) sea la longitud de LCS de las
dos secuencias X e Y. A continuación la definición recursiva de L(X[0..m-1],
Y[0..n-1]).
Si
los últimos caracteres de ambas secuencias coinciden (o X[m-1] == Y[n-1])
entonces
L(X[0..m-1],
Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])
Si
los últimos caracteres de ambas secuencias no coinciden (o X[m-1] != Y[n-1])
entonces
L(X[0..m-1],
Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2])
Ejemplos:
1)
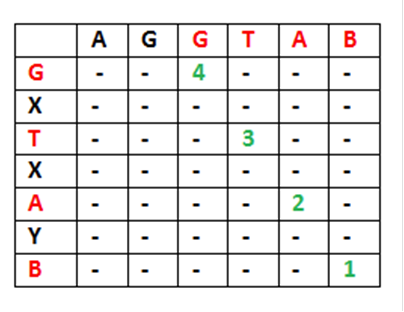
Considere las cadenas de entrada "AGGTAB" y "GXTXAYB". Los
últimos caracteres coinciden con las cadenas. Así que la longitud de LCS puede
ser escrita como:
L("AGGTAB",
"GXTXAYB") = 1 + L("AGGTA", "GXTXAY")
2)
Considerar las cadenas de entrada "ABCDGH" y "AEDFHR". Los
últimos caracteres no coinciden con las cadenas. Así que la longitud de LCS
puede ser escrita como:
L("ABCDGH",
"AEDFHR") = MAX ( L("ABCDG", "AEDFHR"),
L("ABCDGH", "AEDFH") )
Así
que el problema del LCS tiene una propiedad de subestructura óptima ya que el
problema principal puede ser resuelto usando soluciones a los subproblemas.
2)
Subproblemas superpuestos:
Lo
siguiente es una simple implementación recursiva del problema LCS. La
implementación simplemente sigue la estructura recursiva mencionada
anteriormente.
En lenguaje C++:
|
#include <bits/stdc++.h> using namespace std;
int max(int a, int
b); int lcs( char
*X, char *Y, int m, int n ) { if
(m == 0 || n == 0) return 0; if
(X[m-1] == Y[n-1]) return 1 + lcs(X, Y, m-1,
n-1); else return max(lcs(X,
Y, m, n-1), lcs(X, Y, m-1, n)); } int max(int a, int b) { return
(a > b)? a : b; } int main() { char
X[] = "AGGTAB"; char
Y[] = "GXTXAYB"; int
m = strlen(X); int
n = strlen(Y); cout<<"Length of LCS is "<<
lcs( X, Y, m, n ) ; return
0; } Salida: 4 |
La
complejidad temporal del enfoque recursivo sencillo anterior es O(2^n) en el
peor caso y el peor caso ocurre cuando todos los caracteres de X e Y no
coinciden, es decir, la longitud del LCS es 0.
Considerando
la implementación anterior, a continuación se muestra un árbol de recursividad
parcial para las cadenas de entrada "AXYT" y "AYZX".
En
el árbol de recursividad parcial anterior, lcs
("AXY", "AYZ") se está resolviendo dos veces. Si dibujamos
el árbol de recursividad completa, entonces podemos ver que hay muchos subproblemas que se resuelven una y otra vez. Así que este
problema tiene la propiedad Subestructura Superpuesta y la recomposición de los
mismos subproblemas puede evitarse usando la Memotización o la Tabulación. A continuación se muestra una
implementación tabulada para el problema LCS.
#include<bits/stdc++.h>
usando namespace std;
int
max(int a, int b);
/* Devuelve la longitud del LCS para X[0..m-1], Y[0..n-1] */
int
lcs( char *X, char *Y, int m, int n )
{
int
L[m + 1][n + 1];
int
i, j;
/* Los siguientes pasos
construyen L[m+1][n+1] en
la moda de abajo hacia arriba. Tengan en
cuenta que L[i][j]
contiene la longitud
de LCS de X[0..i-1]
y Y[0..j-1] */
para (i = 0; i <= m;
i++)
{
para (j = 0; j <=
n; j++)
{
si (i == 0 || j ==
0)
L[i][j] = 0;
si no, si (X[i - 1]
== Y[j - 1])
L[i][j] = L[i -
1][j - 1] + 1;
más
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
/* L[m][n] contiene la longitud
de LCS
para X[0..n-1] y
Y[0..m-1] */
Devuelve L[m][n];
}
/* Función de utilidad para obtener un máximo de 2 números enteros
*/
int
max(int a, int b)
{
¿Devolver (a > b)? a
: b;
}
// Programa principal
int
main()
{
char
X[] = "AGGTAB";
char
Y[] = "GXTXAYB";
int
m = strlen(X);
int
n = strlen(Y);
cout
<< "La longitud del LCS es "
<< lcs( X, Y, m, n );
return
0;
}
Salida: La longitud del LCS es de 4
La
complejidad temporal de la aplicación anterior es O(mn),
que es mucho mejor que la complejidad temporal del peor de los casos de la
aplicación Recursiva sencilla.
El
algoritmo/código anterior devuelve sólo la longitud del LCS.
2.-
La subsecuencia creciente más larga
Ya
hemos discutido los sub-problemas superpuestos y las propiedades de la
subestructura óptima.
Ahora,
vamos a discutir el problema de la Subsecuencia
Creciente Más Larga (LIS) como un problema de ejemplo que puede ser resuelto
usando la Programación Dinámica.
El
problema de la Mayor Subsecuencia Creciente (LIS) es
encontrar la longitud de la mayor subsecuencia de una
secuencia dada, de tal manera que todos los elementos de la subsecuencia
se ordenen en orden creciente. Por ejemplo, la longitud de LIS para {10, 22, 9,
33, 21, 50, 41, 60, 80} es 6 y LIS es {10, 22, 33, 50, 60, 80}.
Ejemplo:
Entrada:
arr[] = {3, 10, 2, 1, 20}
Salida:
Longitud = 3
La
subsecuencia creciente más larga es 3, 10, 20
Método
Recursivo:
Subestructura
óptima: Dejemos que arr[0..n-1] sea la matriz de
entrada y L(i) sea la longitud del LIS que termina en el índice i, de tal
manera que arr[i] sea el último elemento del LIS.
Entonces,
L(i) puede ser escrita recursivamente como:
L(i)
= 1 + max( L(j) ) donde 0 < j < i y arr[j] < arr[i]; o
L(i)
= 1, si no existe tal j.
Para
encontrar el LIS de un conjunto dado, necesitamos devolver max(L(i))
donde 0 < i < n.
Formalmente,
la longitud de la subsecuente más larga que termina en el índice i, será 1
mayor que el máximo de longitudes de todas las subsecuentes más largas que
terminan en los índices antes de i, donde arr[j] <
arr[i] (j < i). Así pues, vemos que el problema
del SIL satisface la propiedad de subestructura óptima, ya que el problema
principal puede resolverse mediante soluciones a los subproblemas.
El árbol recursivo que se muestra a continuación hará que el enfoque sea más
claro:
Entrada
: arr[] = {3, 10, 2, 11}
f(i):
Denota el LIS del subconjunto que termina en el índice 'i'.
(LIS(1)=1)
f(4) {f(4) = 1 + max(f(1),
f(2), f(3))}
/ | \
f(1)
f(2) f(3) {f(3) = 1, f(2) y f(1) son > f(3)}
| | \
f(1) f(2) f(1) {f(2) = 1 + max(f(1)}
|
f(1) {f(1) = 1}
A
continuación se presenta la aplicación del enfoque recursivo:
#include<stdio.h>
#include<stdlib.h>
int _lis( int arr[], int
n, int *max_ref)
{
if (n == 1)
return 1;
int res, max_ending_here = 1;
for (int
i = 1; i < n; i++)
{
res = _lis(arr, i, max_ref);
if
(arr[i-1] < arr[n-1]
&& res + 1 > max_ending_here)
max_ending_here = res + 1;
}
if (*max_ref
< max_ending_here)
*max_ref
= max_ending_here;
return max_ending_here;
}
int lis(int arr[], int
n)
{
int max
= 1;
_lis( arr, n, &max );
return max;
}
//Principal
int main()
{
int arr[]
= { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = sizeof(arr)/sizeof(arr[0]);
printf("La longitud
es ",
lis( arr, n ));
return 0;
}
Salida: La longitud es 5
Complejidad temporal: La complejidad temporal de este enfoque recursivo es
exponencial, ya que existe un caso de subproblemas
superpuestos como se explica en el diagrama de árbol recursivo anterior.
Espacio Auxiliar: O(1). No se utiliza ningún espacio externo para almacenar
valores aparte del espacio interno de la pila.
3.-
Distancia
Dadas
dos cadenas str1 y str2 y por debajo de las operaciones que se pueden realizar en
str1. Encuentra el mínimo número de ediciones (operaciones) necesarias para
convertir 'str1' en 'str2'.
Insertar
Retire
Reemplazar
Todas
las operaciones anteriores tienen el mismo costo.
Ejemplos:
Entrada:
str1 = "geek", str2 = "gesek"
Salida: 1
Podemos
convertir str1 en str2 insertando una 's'.
¿Cuáles
son los subproblemas en este caso?
La
idea es procesar todos los personajes uno por uno mirando desde el lado
izquierdo o derecho de ambas cuerdas.
Vamos
a atravesar desde la esquina derecha, hay dos posibilidades para cada par de
personajes que se atraviesan.
m:
Longitud de la cadena 1 (primera cadena)
n:
Longitud de la cadena 2 (segunda cadena)
Si
los últimos caracteres de dos cuerdas son iguales, no hay mucho que hacer. Ignorar
los últimos caracteres y obtener la cuenta de las cuerdas restantes. Así que
recurrimos a las longitudes m-1 y n-1.
Si
los últimos caracteres no son iguales, consideramos todas las operaciones en
'str1', consideramos las tres operaciones en el último carácter de la primera
cadena, calculamos recursivamente el coste mínimo de las tres operaciones y
tomamos un mínimo de tres valores.
Insertar:
Recurrir para m y n-1
Quita:
Recurrir para m-1 y n
Reemplazar:
Recurrir para m-1 y n-1
A
continuación se muestra la implementación en C++ de la solución recursiva
ingenua anterior.
#include <bits/stdc++.h>
using namespace
std;
int min(int x, int y, int
z)
{
return min(min(x, y), z);
}
int editDist(string str1, string str2, int m, int n)
{
if (m == 0)
return n;
if (n ==
0) return
m;
if (str1[m - 1] == str2[n - 1])
return editDist(str1,
str2, m - 1, n - 1);
return 1 + min(editDist(str1,
str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1, n - 1) // Replace
);
}
// Principal
int main()
{
string str1 = "sunday";
string str2 = "saturday";
cout << editDist(str1, str2, str1.length(), str2.length());
return 0;
}
Salida: 3
La
complejidad temporal de la solución anterior es exponencial. En el peor de los
casos, podemos terminar haciendo operaciones de O(3m). El peor caso ocurre
cuando ninguno de los caracteres de dos cadenas coinciden. A continuación se
muestra un diagrama de llamada recursivo para el peor caso.
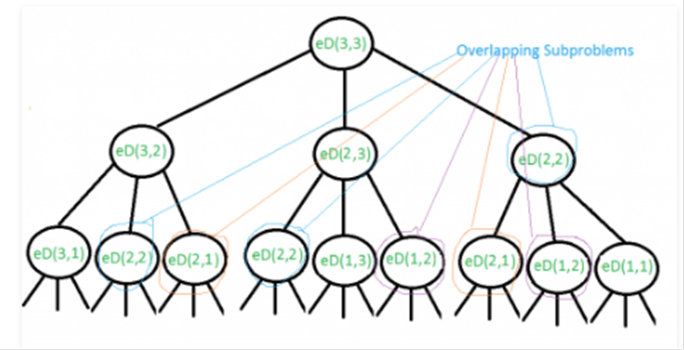
Podemos
ver que muchos subproblemas se resuelven, una y otra
vez, por ejemplo, eD(2, 2) se llama tres veces. Dado
que los mismos suproblemas se llaman de nuevo, este
problema tiene la propiedad Subproblemas
Superpuestos. Por lo tanto, el problema Edit Distance tiene ambas propiedades (ver esto y esto) de un
problema de programación dinámica. Al igual que otros problemas típicos de
Programación dinámica (DP), se pueden evitar los recálculos
de los mismos subproblemas construyendo una matriz
temporal que almacene los resultados de los subproblemas.
4.-
Partición mínima
Dado
un conjunto de números enteros, la tarea consiste en dividirlo en dos conjuntos
S1 y S2 de manera que la diferencia absoluta entre sus sumas sea mínima.
Si
hay un conjunto S con n elementos, entonces si suponemos que el Subconjunto1
tiene m elementos, el Subconjunto2 debe tener n-m elementos y el valor de abs(suma(Subconjunto1) - suma(Subconjunto2)) debe ser
mínimo.
Ejemplo:
Entrada:
arr[] = {1, 6, 11, 5}
Salida:
1
Explicación:
Subconjunto1
= {1, 5, 6}, suma del subconjunto1 = 12
Subconjunto2
= {11}, suma del subconjunto2 = 11
Solución
recursiva
El
enfoque recursivo consiste en generar todas las sumas posibles a partir de
todos los valores de la matriz y comprobar qué solución es la más óptima.
Para
generar las sumas, o bien incluimos el ítem i en el conjunto 1 o no incluimos,
es decir, incluimos en el conjunto 2.
#include <bits/stdc++.h>
using namespace
std;
int findMinRec(int arr[], int
i, int sumCalculated, int sumTotal)
{
if (i==0)
return abs((sumTotal-sumCalculated) - sumCalculated);
return min(findMinRec(arr, i-1, sumCalculated+arr[i-1],
sumTotal),
findMinRec(arr, i-1, sumCalculated, sumTotal));
}
int findMin(int arr[], int
n)
{
int sumTotal
= 0;
for (int
i=0; i<n; i++)
sumTotal
+= arr[i];
return findMinRec(arr, n, 0, sumTotal);
}
//Principal
int main()
{
int arr[]
= {3, 1, 4, 2, 2, 1};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "
La diferencia mínima entre dos conjuntos es
"
<< findMin(arr, n);
return 0;
}
Salida: La diferencia mínima entre dos conjuntos es 1
Todas las sumas pueden ser generadas por
(1) incluyendo ese elemento en el conjunto 1.
(2) sin incluir ese elemento en el conjunto 1.
Así que las posibles combinaciones son :-
arr[0] (1 o 2) -> 2 valores
arr[1] (1 o 2) -> 2
valores
arr[n] (2 o 2) -> 2
valores
Así que la complejidad del tiempo será 2*2*..... *2 (Por n veces),
que es O(2^n).
5.-
Modos de cubrir una distancia
Dada
una distancia, cuente el número total de formas de cubrir la distancia con 1, 2
y 3 pasos.
Ejemplos:
Entrada:
n = 3
Salida:
4
Explicación:
A
continuación están las cuatro formas
1 paso + 1 paso + 1 paso
1 paso + 2 pasos
2 pasos + 1 paso
3 pasos
Entrada:
n = 4
Salida:
7
Explicación:
A
continuación están las cuatro formas
1 paso + 1 paso + 1 paso + 1 paso
1 paso + 2 pasos + 1 paso
2 pasos + 1 paso + 1 paso
1 paso + 1 paso + 2 pasos
2 pasos + 2 pasos
3 pasos + 1 paso
1 paso + 3 pasos
Solución
recursiva
Hay
n escaleras, y una persona puede dar el siguiente paso, saltar una posición o
saltar dos posiciones. Así que hay n posiciones. La idea es pararse en la
posición i, la persona puede moverse por la posición i+1, i+2, i+3. Así que se
puede formar una función recursiva donde en el índice actual i la función se
llama recursivamente para las posiciones i+1, i+2 y i+3.
Hay
otra forma de formar la función recursiva. Para llegar a la posición i, una
persona tiene que saltar desde la posición i-1, i-2 o i-3 donde i es la
posición inicial.
Algoritmo:
Crear
una función recursiva (count(int
n)) que toma un solo parámetro.
Comprueba
los casos base. Si el valor de n es menor que 0 entonces devuelve 0, y si el
valor de n es igual a cero entonces devuelve 1 ya que es la posición inicial.
Llama
a la función de forma recursiva con los valores n-1, n-2 y n-3 y suma los
valores que se devuelven, es decir, suma = cuenta(n-1) + cuenta(n-2) +
cuenta(n-3).
Devuelve
el valor de la suma.
Implementación:
|
#include<iostream>
using namespace
std; int printCountRec(int dist) { if (dist<0)
return 0; if (dist==0)
return 1; return printCountRec(dist-1) + printCountRec(dist-2) + printCountRec(dist-3); } // Principal int main()
{ int dist
= 4; cout << printCountRec(dist); return 0; } |
Salida: 7
Complejidad
temporal: O(3n).
La
complejidad temporal de la solución anterior es exponencial, un límite superior
cercano es O(3n). De cada estado 3, se llama una función recursiva. Así que el
límite superior para n estados es O(3n).
Complejidad
espacial: O(1).
No
se requiere espacio adicional.
6.-
El camino más largo de la matriz
Dada
una matriz de n*n donde todos los números son distintos, encuentre el camino de
máxima longitud (empezando por cualquier célula) de tal manera que todas las
células a lo largo del camino estén en orden creciente con una diferencia de 1.
Podemos
movernos en 4 direcciones desde una célula dada (i, j), es decir, podemos
movernos a (i+1, j) o (i, j+1) o (i-1, j) o (i, j-1) con la condición de que
las células adyacentes tengan una diferencia de 1.
Ejemplo:
Entrada:
mat[][] = {{1, 2, 9}
{5, 3, 8}
{4, 6, 7}}
Salida:
4
El
camino más largo es el 6-7-8-9.
La
idea es sencilla; calculamos el camino más largo empezando por cada célula. Una
vez que hayamos calculado el más largo para todas las células, regresamos el
máximo de todos los caminos más largos. Una observación importante en este
enfoque es que muchos subproblemas se superponen. Por
lo tanto, este problema puede ser resuelto de manera óptima usando la
Programación Dinámica.
A
continuación se muestra la implementación basada en la Programación Dinámica
que utiliza una tabla de búsqueda dp[][] para comprobar
si un problema ya está resuelto o no.
#include <bits/stdc++.h>
#define n 3
using namespace
std;
int findLongestFromACell(int i, int j, int
mat[n][n], int dp[n][n])
{
if (i < 0 || i >= n
|| j < 0 || j >= n) return
0;
if (dp[i][j]
!= -1) return dp[i][j];
int x = INT_MIN, y = INT_MIN,
z = INT_MIN, w = INT_MIN;
if (j < n - 1
&& ((mat[i][j] + 1) == mat[i][j
+ 1]))
x = 1 + findLongestFromACell(i,
j + 1, mat, dp);
if (j > 0 && (mat[i][j] + 1 == mat[i][j - 1]))
y = 1 + findLongestFromACell(i,
j - 1, mat, dp);
if (i > 0 && (mat[i][j] + 1 == mat[i - 1][j]))
z = 1 + findLongestFromACell(i
- 1, j, mat, dp);
if (i < n - 1
&& (mat[i][j] + 1 == mat[i
+ 1][j]))
w = 1 + findLongestFromACell(i
+ 1, j, mat, dp);
return dp[i][j] = max(x, max(y, max(z, max(w,
1))));
}
int finLongestOverAll(int mat[n][n])
{
int result
= 1; // Initialize result
int dp[n][n];
memset(dp, -1, sizeof dp);
for (int
i = 0; i < n; i++) {
for
(int j = 0; j < n; j++)
{
if (dp[i][j] == -1)
findLongestFromACell(i, j, mat, dp);
result = max(result,
dp[i][j]);
}
}
return result;
}
// Principal
int main()
{
int mat[n][n]
= { { 1, 2, 9 },
{
5, 3, 8 },
{
4, 6, 7 } };
cout << " La
longitud del camino más largo es de "
<< finLongestOverAll(mat);
return 0;
}
Salida: La longitud del camino más largo es de 4
La complejidad temporal de la solución anterior es O(n2). Puede parecer más
a primera vista. Si miramos más de cerca, podemos notar que todos los valores
de dp[i][j] se calculan sólo una vez.
7.-
Problema de la suma de subconjuntos
Dado
un conjunto de números enteros no negativos, y una suma de valores, determinar
si hay un subconjunto del conjunto dado con una suma igual a la suma dada.
Ejemplo:
Entrada:
conjunto[] = {3, 34, 4, 12, 5, 2}, suma = 9
Salida:
Verdadero
Hay
un subconjunto (4, 5) con la suma 9.
Método
Recursivo:
Para
el enfoque recursivo consideraremos dos casos.
Consideremos
el último elemento y ahora la suma requerida = suma objetivo - valor del
"último" elemento y número de elementos = total de elementos - 1
Deje
el "último" elemento y ahora la suma requerida = suma objetivo y
número de elementos = total de elementos - 1
A
continuación la fórmula recursiva para el problema de isSubsetSum().
isSubsetSum(set,
n, sum)
=
isSubsetSum(set, n-1, sum) ||
isSubsetSum(set,
n-1, sum-set[n-1])
Casos
base:
isSubsetSum(set,
n, sum) = falso, si la suma > 0 y n == 0
isSubsetSum(set,
n, sum) = true, if sum == 0
Echemos
un vistazo a la simulación de la aproximación anterior..:
set[]={3,
4, 5, 2}
suma=9
(x,
y)= 'x' es el número de elementos de la izquierda,
"y"
es la suma requerida
(4, 9)
{Verdad}
/ \
(3, 6) (3, 9)
/ \ / \
(2, 2) (2, 6) (2, 5) (2, 9)
{Verdad}
/ \
(1, -3) (1, 2)
{Falso}
{Verdadero}
/ \
(0, 0) (0, 2)
{Verdadero} {Falso}
#include <stdio.h>
bool isSubsetSum(int set[], int n, int sum)
{
// Base Cases
if (sum == 0)
return
true;
if (n == 0)
return
false;
if (set[n - 1] > sum)
return isSubsetSum(set,
n - 1, sum);
return isSubsetSum(set, n - 1, sum)
|| isSubsetSum(set, n - 1, sum - set[n - 1]);
}
// Principal
int main()
{
int set[] = { 3, 34, 4,
12, 5, 2 };
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if (isSubsetSum(set,
n, sum) == true)
printf("Encontré
un subconjunto con una suma dada ");
else
printf("No
encontré un subconjunto con una suma dada ");
return 0;
}
Salida: Encontré un subconjunto con una suma dada
Complejidad: La solución anterior puede probar todos los subconjuntos de un
determinado conjunto en el peor de los casos. Por lo tanto, la complejidad
temporal de la solución anterior es exponencial. El problema es de hecho
NP-Completo
8.-
Estrategia óptima para un juego
Considere
una fila de n monedas de valores v1 . . . vn, donde n
es par. Jugamos una partida contra un oponente alternando turnos. En cada
turno, un jugador selecciona la primera o la última moneda de la fila, la
retira de la fila permanentemente y recibe el valor de la moneda. Determina la
máxima cantidad de dinero posible que podemos ganar definitivamente si nos
movemos primero.
Nota:
El oponente es tan inteligente como el usuario.
Entendamos
el problema con algunos ejemplos:
5,
3, 7, 10 : El usuario recoge el valor máximo como 15(10 + 5)
8,
15, 3, 7 : El usuario recoge el valor máximo como 22(7 + 15)
¿Elegir
lo mejor en cada movimiento da una solución óptima? No.
En
el segundo ejemplo, así es como se puede terminar el juego:
.......El
usuario elige 8.
.......El
usuario elige 15.
.......El
usuario elige 7.
.......El
opositor elige 3.
El
valor total recogido por el usuario es 15(8 + 7)
.......El
usuario elige 7.
.......El
usuario elige 8.
.......El
usuario elige 15.
.......El
opositor elige 3.
El
valor total recogido por el usuario es 22(7 + 15)
Así
que si el usuario sigue el segundo estado de juego, el valor máximo puede ser
recogido aunque el primer movimiento no sea el mejor.
Como
ambos jugadores son igual de fuertes, ambos intentarán reducir la posibilidad
de ganarse el uno al otro. Ahora veamos cómo el oponente puede lograr esto.
Hay
dos opciones:
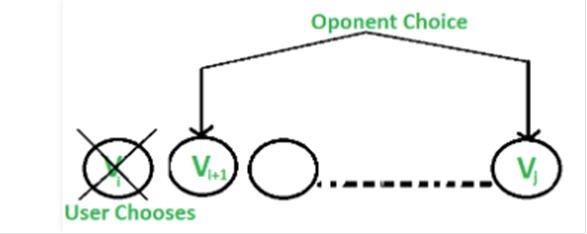
El
usuario elige la moneda "i" con el valor "Vi": El oponente
elige la moneda "i+1" o la moneda "j". El oponente tiene la
intención de elegir la moneda que deja al usuario con un valor mínimo.
Es
decir, el usuario puede recoger el valor Vi + min(F(i+2, j), F(i+1, j-1) ).
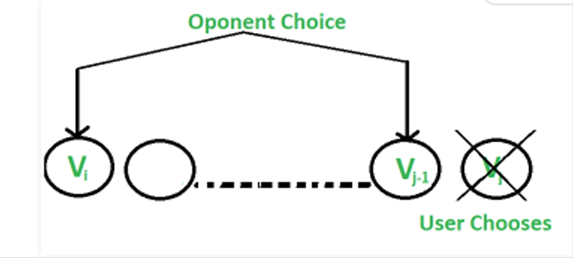
El
usuario elige la moneda 'jth' con valor 'Vj': El oponente elige la moneda 'ith'
o la 'j-1'. El oponente tiene la intención de elegir la moneda que deja al
usuario con un valor mínimo, es decir, el usuario puede recoger el valor Vj + min(F(i+1, j-1), F(i, j-2) ).
A
continuación se presenta la solución recursiva que se basa en las dos opciones
anteriores. Tomamos un máximo de dos opciones.
F(i,
j) representa el valor máximo que el usuario
puede
recoger desde la moneda I'th hasta la J'th.
F(i,
j) = Max(Vi + min(F(i+2, j), F(i+1, j-1) ),
Vj +
min(F(i+1, j-1), F(i, j-2) ))
Como
usuario quiere maximizar el número de monedas.
Casos
de base
F(i, j) = Vi Si j == i
F(i, j) = max(Vi,
Vj) Si j == i + 1
#include <bits/stdc++.h>
using namespace
std;
int optimalStrategyOfGame(
int* arr,
int n)
{
int table[n][n];
for (int
gap = 0; gap < n; ++gap) {
for
(int i = 0, j = gap; j < n; ++i, ++j) {
int x = ((i + 2) <= j)
?
table[i + 2][j]
:
0;
int y = ((i + 1) <= (j - 1))
?
table[i + 1][j - 1]
:
0;
int z = (i <= (j - 2))
?
table[i][j - 2]
:
0;
table[i][j] = max(
arr[i] + min(x, y),
arr[j] + min(y, z));
}
}
return table[0][n - 1];
}
// Principal
int main()
{
int arr1[] = { 8, 15, 3,
7 };
int n = sizeof(arr1) / sizeof(arr1[0]);
printf("%d\n",
optimalStrategyOfGame(arr1, n));
int arr2[] = { 2, 2, 2, 2
};
n = sizeof(arr2) / sizeof(arr2[0]);
printf("%d\n",
optimalStrategyOfGame(arr2, n));
int arr3[] = { 20, 30, 2,
2, 2, 10 };
n = sizeof(arr3) / sizeof(arr3[0]);
printf("%d\n",
optimalStrategyOfGame(arr3, n));
return 0;
}
Salida: 22 4 42
Complejidad: O(n2).
El uso de un bucle anidado para el bucle lleva la complejidad del tiempo a
n2.
Espacio auxiliar: O(n2).
Como una tabla 2-D se utiliza para almacenar estados.
9.-
Problema de la mochila
Dado
el peso y el valor de n artículos, colóquelos en una mochila de capacidad W
para obtener el máximo valor total en la mochila. En otras palabras, dados dos
conjuntos de números enteros val[0..n-1] y wt[0..n-1]
que representan valores y pesos asociados a n artículos respectivamente.
También dado un entero W que representa la capacidad de la mochila, averigua el
máximo valor del subconjunto de val[] de tal manera que la suma de los pesos de
este subconjunto sea menor o igual que W. No puedes romper un artículo, ni
escoger el artículo completo ni no escogerlo (propiedad 0-1).
Problema
de la mochila:

Método
Recursivo:
Una
solución simple es considerar todos los subconjuntos de artículos y calcular el
peso y el valor total de todos los subconjuntos. Considere los únicos
subconjuntos cuyo peso total es menor que W. De todos esos subconjuntos, elija
el subconjunto de valor máximo.
Subestructura
óptima: Para considerar todos los subconjuntos de artículos, puede haber dos
casos para cada artículo.
Caso
1: El artículo está incluido en el subconjunto óptimo.
Caso
2: El artículo no está incluido en el conjunto óptimo.
Por
lo tanto, el valor máximo que se puede obtener de "n" artículos es el
máximo de los dos valores siguientes.
Valor
máximo obtenido por n-1 artículos y peso W (excluyendo n-ésimo
artículo).
Valor
del n-ésimo artículo más el valor máximo obtenido por
n-1 artículos y W menos el peso del n-ésimo artículo
(incluido el n-ésimo artículo).
Si
el peso del artículo "n-ésimo" es mayor que
el de "W", entonces el artículo n-ésimo no
puede incluirse y el caso 1 es la única posibilidad.
A
continuación se presenta la aplicación del enfoque anterior:
#include <bits/stdc++.h>
using namespace
std;
int max(int a, int b) { return (a > b) ? a : b; }
int knapSack(int W, int wt[],
int val[], int n)
{
if (n == 0 || W == 0)
return 0;
if (wt[n]
> W) return knapSack(W,
wt, val, n - 1);
else
return
max(
val[n]
+ knapSack(W - wt[n],
wt, val, n - 1),
knapSack(W, wt, val, n - 1));
}
// Principal
int main()
{
int val[] = { 60, 100,
120 };
int wt[]
= { 10, 20, 30 };
int W = 50;
int n = sizeof(val) / sizeof(val[0]);
cout << knapSack(W, wt, val, n);
return 0;
}
Salida: 220
Cabe
señalar que la función anterior calcula los mismos subproblemas
una y otra vez. Véase el siguiente árbol de recursividad, K(1, 1) se evalúa dos
veces. La complejidad temporal de esta solución recursiva ingenua es
exponencial (2^n).
En
el siguiente árbol de recursión, K() se refiere a
a
KnapSack. Los dos parámetros indicados en el
El
siguiente árbol de recursividad son la n y la W.
El
árbol de recursividad es para las siguientes entradas de muestra.
wt[]
= {1, 1, 1}, W = 2, val[] = {10, 20, 30}
K(n, W)
K(3, 2)
/ \
/ \
K(2, 2) K(2, 1)
/ \ / \
/ \ / \
K(1, 2) K(1, 1) K(1, 1) K(1, 0)
/ \ / \ / \
/ \ / \ / \
K(0,
2) K(0, 1) K(0, 1) K(0, 0) K(0, 1) K(0, 0)
Árbol
de recursividad para la capacidad de la mochila 2
y
3 artículos de 1 unidad de peso.
Complejidad:
O(2^n).
Como
hay subproblemas redundantes.
Espacio
auxiliar :O(1).
Como
no se ha utilizado ninguna estructura de datos extra para almacenar valores.
10.-
Problema de parentesco booleano
Dada
una expresión booleana con los siguientes símbolos.
Símbolos
"T"... cierto...
F' ---> falso
Y
los siguientes operadores llenos entre los símbolos
Operadores
& ---> booleano Y
||> booleano O
^ ---> booleano XOR
Cuente
el número de formas en que podemos poner entre paréntesis la expresión para que
el valor de la expresión se evalúe como verdadero.
Dejemos
que la entrada sea en forma de dos matrices, una que contenga los símbolos (T y
F) en orden y otra que contenga los operadores (&, | y ^}
Ejemplos:
Entrada:
símbolo[] = {T, F, T}
operador[] = {^, &}
Salida:
2
La
expresión dada es "T ^ F & T", evalúa la verdadera
de
dos maneras "((T ^ F) & T)" y "(T ^ (F & T))"
Casos:
T(i,
i) = 1 si el símbolo[i] = "T
T(i,
i) = 0 si el símbolo[i] = 'F'.
F(i,
i) = 1 si el símbolo[i] = "F
F(i,
i) = 0 si el símbolo[i] = 'T'.
Si
dibujamos el árbol de recursividad de la solución recursiva anterior, podemos
observar que tiene muchos subproblemas superpuestos. Como
otros problemas de programación dinámica, puede ser resuelto llenando una tabla
de abajo hacia arriba. A continuación se muestra la implementación en C++ de la
solución de programación dinámica.
#include<iostream>
#include<cstring>
using namespace
std;
int countParenth(char symb[], char
oper[], int n)
{
int F[n][n], T[n][n];
for (int
i = 0; i < n; i++)
{
F[i][i] = (symb[i] == 'F')? 1: 0;
T[i][i] = (symb[i] == 'T')? 1: 0;
}
for (int
gap=1; gap<n; ++gap)
{
for
(int i=0, j=gap; j<n; ++i, ++j)
{
T[i][j]
= F[i][j] = 0;
for (int g=0; g<gap; g++)
{
int k = i + g;
int tik = T[i][k] + F[i][k];
int tkj = T[k+1][j] + F[k+1][j];
if (oper[k] == '&')
{
T[i][j]
+= T[i][k]*T[k+1][j];
F[i][j]
+= (tik*tkj -
T[i][k]*T[k+1][j]);
}
if (oper[k] == '|')
{
F[i][j]
+= F[i][k]*F[k+1][j];
T[i][j]
+= (tik*tkj -
F[i][k]*F[k+1][j]);
}
if (oper[k] == '^')
{
T[i][j]
+= F[i][k]*T[k+1][j] + T[i][k]*F[k+1][j];
F[i][j]
+= T[i][k]*T[k+1][j] + F[i][k]*F[k+1][j];
}
}
}
}
return T[0][n-1];
}
//Principal
int main()
{
char symbols[] =
"TTFT";
char operators[]
= "|&^";
int n = strlen(symbols);
cout << countParenth(symbols, operators,
n);
return 0;
}
Salida: 4
Complejidad: O(n3)
Espacio auxiliar: O(n2)
&&&&&&&&&&&&&
&&&&&&&&&&
&&&
&