

LOS
10 MEJORES ALGORITMOS DE GRAFOS
&&&&&&&&&&
&&&&&&&
&&&
&
1.- Breadth First Search o BFS para un grAFo
Breadth
First Traversal (o Búsqueda) para un gráfico es similar a Breadth First Traversal
de un árbol. La única pega aquí es que, a diferencia de los árboles, los
gráficos pueden contener ciclos, por lo que podemos llegar al mismo nodo de
nuevo. Para evitar procesar un nodo más de una vez, usamos una matriz booleana
visitada. Para simplificar, se asume que todos los vértices son accesibles
desde el vértice inicial.
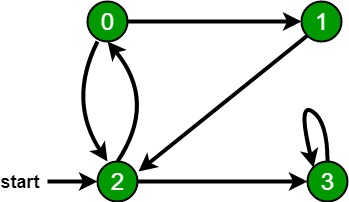
Por
ejemplo, en el siguiente gráfico, empezamos a recorrer desde el vértice 2.
Cuando llegamos al vértice 0, buscamos todos los vértices adyacentes del mismo.
2 es también un vértice adyacente de 0. Si no marcamos los vértices visitados,
entonces 2 se procesará de nuevo y se convertirá en un proceso no terminante.
La amplitud de la primera travesía del siguiente gráfico es 2, 0, 3, 1.
A
continuación se presentan las implementaciones de la simple "Breadth First
Traversal" de una fuente determinada.
La
implementación utiliza la representación de la lista de adyacencia de los
gráficos. El contenedor de listas de STL se utiliza para almacenar listas de
nodos adyacentes y cola de nodos necesarios para la travesía de BFS.
|
#include<iostream> #include <list> using namespace std; class Graph { int
V; // No. de vertices // Puntero a la
matriz lists list<int>
*adj; public: Graph(int V); //
Constructor //
función profundidad gráfico void addEdge(int v,
int w); void BFS(int
s); }; Graph::Graph(int V) { this->V = V; adj = new
list<int>[V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w);
// Add w to v’s list. } void Graph::BFS(int s) { // vertices no
visitados bool *visited = new
bool[V]; for(int i = 0; i
< V; i++) visited[i] = false; list<int>
queue; visited[s] = true; queue.push_back(s); list<int>::iterator
i; while(!queue.empty())
{ s
= queue.front(); cout
<< s << " "; queue.pop_front();
for
(i = adj[s].begin(); i != adj[s].end(); ++i) {
if
(!visited[*i]) {
visited[*i]
= true; queue.push_back(*i);
}
}
} } //Programa principal int main() { Graph g(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.addEdge(3, 3); cout <<
"Lo siguiente es Breadth First Traversal " <<
"(starting from vertex 2) \n"; g.BFS(2); return 0; } |
Salida: 2031
Ilustración:
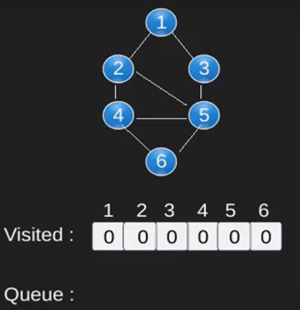
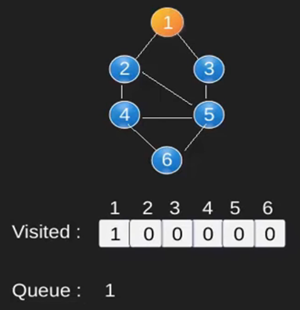
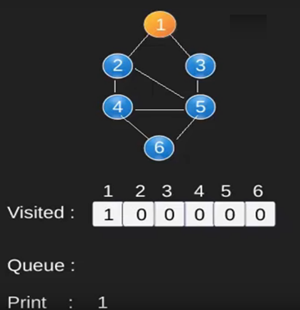
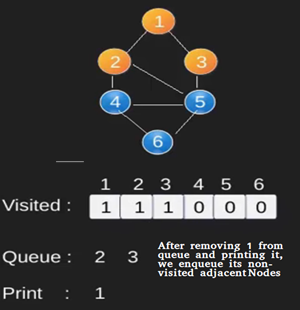
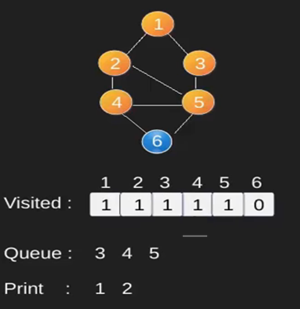
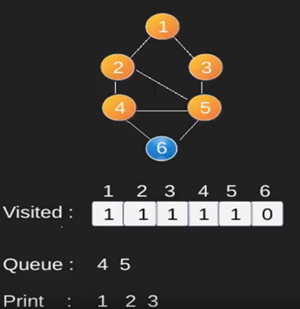
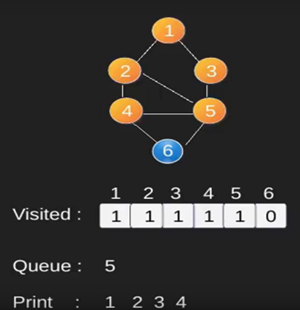
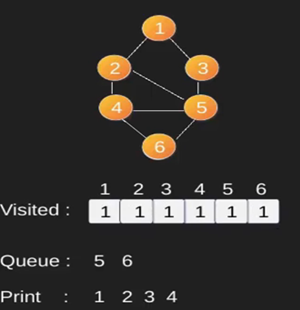
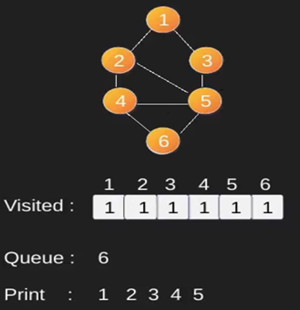
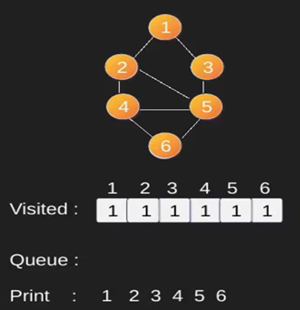
Obsérvese
que el código anterior sólo atraviesa los vértices accesibles desde un vértice
de origen determinado. Puede que no se pueda acceder a todos los vértices desde
un vértice determinado (ejemplo Gráfico desconectado). Para imprimir todos los
vértices, podemos modificar la función BFS para que haga la travesía empezando
por todos los nodos uno a uno (como la versión modificada de DFS) .
Complejidad
del tiempo: O(V+E) donde V es el número de vértices en el gráfico y E es el
número de aristas en el gráfico.
2.-
Profundidad Primera Búsqueda o DFS para un grAFo
Profundidad
Primera Travesía (o Búsqueda) para un gráfico es similar a Profundidad Primera
Travesía de un árbol. La única pega aquí es que, a diferencia de los árboles,
los gráficos pueden contener ciclos, un nodo puede ser visitado dos veces. Para
evitar procesar un nodo más de una vez, usa una matriz booleana visitada.
Ejemplo:
Entrada:
n = 4, e = 6
0
-> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Salida:
DFS del vértice 1 : 1 2 0 3
La
búsqueda de profundidad primero es un algoritmo para atravesar o buscar
estructuras de datos de árboles o gráficos. El algoritmo comienza en el nodo
raíz (seleccionando algún nodo arbitrario como nodo raíz en el caso de un
gráfico) y explora en la medida de lo posible a lo largo de cada rama antes de
retroceder. Así que la idea básica es empezar desde la raíz o cualquier nodo
arbitrario y marcar el nodo y moverse al nodo adyacente sin marcar y continuar
este bucle hasta que no haya ningún nodo adyacente sin marcar. Luego retroceder
y comprobar si hay otros nodos sin marcar y atravesarlos. Finalmente imprime
los nodos en el camino.
Algoritmo:
Crea
una función recursiva que toma el índice de nodo y una matriz visitada.
Marca
el nodo actual como visitado e imprime el nodo.
Atravesar
todos los nodos adyacentes y no marcados y llamar a la función recursiva con el
índice del nodo adyacente.
#include<bits/stdc++.h>
using namespace std;
class Graph
{
int V; // No. of vertices
list<int> *adj;
void DFSUtil(int v, bool visited[]);
public:
Graph(int V); // Constructor
void addEdge(int v, int w);
void DFS(int v);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
void Graph::DFSUtil(int v, bool visited[])
{
visited[v] = true;
cout << v << " ";
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i,
visited);
}
void Graph::DFS(int v)
{
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
DFSUtil(v, visited);
}
int main()
{
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << " A continuación se muestra la
profundidad de la primera travesía (a partir del vértice 2) \n";
g.DFS(2);
return 0;
}
Salida:
A continuación se muestra la profundidad de la primera travesía (a partir
del vértice 2) 2 0 1 3
Análisis de la complejidad:
Complejidad
temporal: O(V + E), donde
V es el número de vértices y E es el número de aristas en el gráfico.
Complejidad espacial: O(V).
Ya que, se necesita un conjunto extra visitado de tamaño V.
3.-
El camino más corto desde la fuente a todos los vértices *Dijkstra*
Dado
un gráfico y un vértice de origen en el gráfico, encontrar los caminos más
cortos desde el origen hasta todos los vértices en el gráfico dado.
El
algoritmo de Dijkstra es muy similar al algoritmo de Prim para el árbol de
extensión mínima. Como el MST de Prim, generamos un SPT (árbol de camino más
corto) con la fuente dada como raíz. Mantenemos dos conjuntos, un conjunto
contiene vértices incluidos en el árbol de camino más corto, otro conjunto
incluye vértices aún no incluidos en el árbol de camino más corto. En cada paso
del algoritmo, encontramos un vértice que está en el otro conjunto (conjunto de
no incluidos todavía) y tiene una distancia mínima de la fuente.
A
continuación se detallan los pasos utilizados en el algoritmo de Dijkstra para
encontrar el camino más corto desde un único vértice de la fuente a todos los
demás vértices del gráfico dado.
Algoritmo
1)
Crear un conjunto sptSet (conjunto de árbol de camino más corto) que lleve un
registro de los vértices incluidos en el árbol de camino más corto, es decir, cuya
distancia mínima desde la fuente se calcula y finaliza. Inicialmente, este
conjunto está vacío.
2)
Asigne un valor de distancia a todos los vértices del gráfico de entrada.
Inicialice todos los valores de distancia como INFINITO. Asigne el valor de distancia
como 0 para el vértice de la fuente, de modo que se elija primero.
3)
Aunque sptSet no incluye todos los vértices
....a)
Escoge un vértice u que no esté en sptSet y que tenga un valor de distancia
mínima.
....b)
Incluya u en el sptSet.
....c)
Actualiza el valor de distancia de todos los vértices adyacentes de u. Para
actualizar los valores de distancia, itera a través de todos los vértices
adyacentes. Para cada vértice adyacente v, si la suma del valor de distancia de
u (de la fuente) y el peso del borde u-v, es menor que el valor de distancia de
v, entonces actualiza el valor de distancia de v.
Utilizamos
una matriz booleana sptSet[] para representar el conjunto de vértices incluidos
en SPT. Si un valor sptSet[v] es verdadero, entonces el vértice v está incluido
en SPT, de lo contrario no. La matriz dist[] se utiliza para almacenar los
valores de distancia más corta de todos los vértices.
#include <limits.h>
#include <stdio.h>
#define V 9
int minDistance(int dist[], bool sptSet[])
{
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false
&& dist[v] <= min)
min
= dist[v], min_index = v;
return min_index;
}
void printSolution(int dist[])
{
printf("Vertex \t\t Distance from
Source\n");
for (int i = 0; i < V; i++)
printf("%d \t\t
%d\n", i, dist[i]);
}
void dijkstra(int graph[V][V], int src)
{
int dist[V];
bool sptSet[V];
for (int i = 0; i < V; i++)
dist[i] = INT_MAX, sptSet[i]
= false;
dist[src] = 0;
for (int count = 0; count < V - 1; count++) {
int u = minDistance(dist,
sptSet);
sptSet[u] = true;
for (int v = 0; v < V;
v++)
if
(!sptSet[v] && graph[u][v] && dist[u] != INT_MAX
&&
dist[u] + graph[u][v] < dist[v])
dist[v]
= dist[u] + graph[u][v];
}
printSolution(dist);
}
int main()
{
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{
4, 0, 8, 0, 0, 0, 0, 11, 0 },
{
0, 8, 0, 7, 0, 4, 0, 0, 2 },
{
0, 0, 7, 0, 9, 14, 0, 0, 0 },
{
0, 0, 0, 9, 0, 10, 0, 0, 0 },
{
0, 0, 4, 14, 10, 0, 2, 0, 0 },
{
0, 0, 0, 0, 0, 2, 0, 1, 6 },
{
8, 11, 0, 0, 0, 0, 1, 0, 7 },
{
0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}
Vértice Distancia de la fuente
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
Notas:
1) El código calcula la distancia más corta, pero no calcula la información
del camino. Podemos crear una matriz matriz matriz, actualizar la matriz matriz
matriz cuando se actualiza la distancia (como la implementación de prim) y
usarla para mostrar el camino más corto desde el origen hasta los diferentes
vértices.
2) El código es para el gráfico no dirigido, la misma función dijkstra
puede ser usada para los gráficos dirigidos también.
3) El código encuentra las distancias más cortas desde la fuente a todos
los vértices. Si sólo nos interesa la distancia más corta desde la fuente hasta
un solo objetivo, podemos romper el bucle para el bucle cuando el vértice de
distancia mínima elegido sea igual al objetivo (Paso 3.a del algoritmo).
4) La complejidad temporal de la implementación es O(V^2). Si el gráfico de
entrada se representa con la lista de adyacencias, puede reducirse a O(E log V)
con la ayuda de la pila binaria. Por favor, vea
Algoritmo de Dijkstra para la representación de la lista de adyacencia para
más detalles.
5) El algoritmo de Dijkstra no funciona para gráficos con bordes de peso
negativo. Para los gráficos con bordes de peso negativo, se puede usar el
algoritmo de Bellman-Ford, pronto lo discutiremos en un post separado.
4.-
El camino más corto de cada vértice a otro vértice *Floyd Warshall*
El
algoritmo de Floyd Warshall es para resolver el problema del camino más corto
de todos los pares. El problema es encontrar las distancias más cortas entre
cada par de vértices en un determinado gráfico dirigido ponderado de borde.
Ejemplo:
Entrada:
graph[][] = { {0, 5,
INF, 10},
{INF, 0,
3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0} }
que
representa el siguiente gráfico:
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3
Observe
que el valor del gráfico[i][j] es 0 si i es igual a j
Y
el gráfico[i][j] es INF (infinito) si no hay un borde desde el vértice i a j.
Salida:
Corto
distancia matriz
0
5 8 9
INF
0 3 4
INF
INF 0 1
INF
INF INF 0
Algoritmo
de Floyd Warshall
Inicializamos
la matriz de solución igual que la matriz del gráfico de entrada como primer
paso. Luego actualizamos la matriz de solución considerando todos los vértices
como un vértice intermedio. La idea es elegir uno a uno todos los vértices y
actualizar todos los caminos más cortos que incluyen el vértice elegido como
vértice intermedio en el camino más corto. Cuando elegimos el vértice número k
como un vértice intermedio, ya hemos considerado los vértices {0, 1, 2, .. k-1}
como vértices intermedios. Para cada par (i, j) de los vértices origen y
destino respectivamente, hay dos casos posibles.
1)
k no es un vértice intermedio en el camino más corto de i a j. Mantenemos el
valor de dist[i][j] tal como está.
2)
k es un vértice intermedio en el camino más corto de i a j. Actualizamos el
valor de dist[i][j] como dist[i][k] + dist[k][j] si dist[i][j] > dist[i][k]
+ dist[k][j]
La
siguiente figura muestra la propiedad de la subestructura óptima anterior en el
problema del camino más corto de todos los pares.

#include <bits/stdc++.h>
using namespace std;
#define V 4
#define INF 99999
void printSolution(int dist[][V]);
void floydWarshall (int graph[][V])
{
/* dist[][] será la matriz de salida
que finalmente tendrá el más
corto
distancias entre cada par de
vértices */
int dist[V][V], i, j, k;
/* Inicializar la matriz de solución misma
como matriz de gráficos de
entrada. O podemos decir
los valores iniciales de las
distancias más cortas
se basan en los caminos más
cortos considerando
no hay vértice intermedio
. */
for (i = 0; i < V; i++)
for (j = 0; j < V;
j++)
dist[i][j]
= graph[i][j];
/* Sume todos los vértices uno por uno a
el conjunto de vértices
intermedios.
---> Antes del comienzo de una
iteración,
tenemos las distancias más cortas
entre todos
pares de vértices tales que
el
Las distancias más cortas
consideran sólo la
vértices en el conjunto {0, 1, 2,
.. k-1} como
vértices intermedios.
----> Después del final de una
iteración,
el vértice no. k se añade al
conjunto de
vértices intermedios y el
conjunto se convierte en {0, 1, 2, .. k}
*/
for (k = 0; k < V; k++)
{
// Pick all vertices as
source one by one
for (i = 0; i < V;
i++)
{
for
(j = 0; j < V; j++)
{
if
(dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j]
= dist[i][k] + dist[k][j];
}
}
}
printSolution(dist);
}
void printSolution(int dist[][V])
{
cout<<"The following matrix shows the
shortest distances"
"
between every pair of vertices \n";
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V;
j++)
{
if
(dist[i][j] == INF)
cout<<"INF"<<"
";
else
cout<<dist[i][j]<<"
";
}
cout<<endl;
}
}
// Principal
int main()
{
/* Vamos a crear el siguiente
gráfico ponderado
10
(0)------->(3)
|
/|\
5 | |
| |
1
\|/ |
(1)------->(2)
3
*/
int graph[V][V] = { {0, 5, INF, 10},
{INF,
0, 3, INF},
{INF,
INF, 0, 1},
{INF,
INF, INF, 0}
};
floydWarshall(graph);
return 0;
}
Salida:
La siguiente matriz muestra las distancias más cortas
entre cada par de vértices
0 5
8 9
INF 0
3 4
INF INF
0 1
INF INF
INF 0
Complejidad temporal: O(V^3)
5.-
Detectar el ciclo en un grafo *Union Find*
Una
estructura de datos de conjunto desarticulado es una estructura de datos que
hace un seguimiento de un conjunto de elementos divididos en varios
subconjuntos desarticulados (no superpuestos). Un algoritmo de búsqueda de
unión es un algoritmo que realiza dos operaciones útiles en dicha estructura de
datos:
Resolver:
Determinar en qué subconjunto se encuentra un elemento en particular. Esto
puede utilizarse para determinar si dos elementos están en el mismo
subconjunto.
Unión:
Unir dos subconjuntos en un solo subconjunto.
Discutiremos
la aplicación de la Estructura de Datos de Conjuntos Desconectados. La
aplicación es para comprobar si un gráfico dado contiene un ciclo o no.
El
Algoritmo Union-Find puede ser usado para comprobar si un gráfico no dirigido
contiene un ciclo o no. Note que hemos discutido un algoritmo para detectar el
ciclo. Este es otro método basado en Union-Find. Este método asume que el
gráfico no contiene ningún auto-ciclo.
Podemos
hacer un seguimiento de los subconjuntos en una matriz 1D, llamémosla parent[].
Consideramos
el grafo:
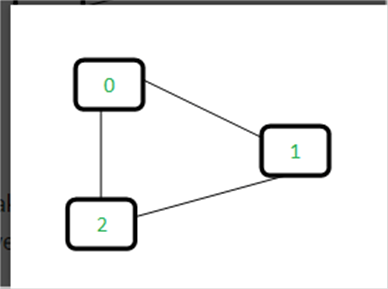
Para
cada borde, haga subconjuntos usando los dos vértices del borde. Si ambos
vértices están en el mismo subconjunto, se encuentra un ciclo.
Inicialmente,
todas las ranuras de la matriz matriz matriz se inicializan a -1 (significa que
sólo hay un elemento en cada subconjunto).
0 1 2
-1
-1 -1
Ahora
procesa todos los bordes uno por uno.
Borde
0-1: Encuentra los subconjuntos en los que están los vértices 0 y 1. Como están
en diferentes subconjuntos, tomamos la unión de ellos. Para tomar la unión, o
bien hacemos el nodo 0 como padre del nodo 1 o viceversa.
0
1 2 <----- 1 se hace padre de 0 (1 es ahora representativo del subconjunto
{0, 1})
1
-1 -1
Borde
1-2: 1 está en el subconjunto 1 y 2 está en el subconjunto 2. Así que, toma la
unión.
0
1 2 <----- 2 se hace padre de 1 (2 es ahora representativo del subconjunto
{0, 1, 2})
1
2 -1
Borde
0-2: 0 está en el subconjunto 2 y 2 está también en el subconjunto 2. Por lo tanto,
incluir este borde forma un ciclo.
¿Cómo
es que el subconjunto 0 es igual al 2?
0->1->2
// 1 es el padre de 0 y 2 es el padre de 1
#include <bits/stdc++.h>
using namespace std;
class Edge
{
public:
int src, dest;
};
class Graph
{
public:
int V, E;
Edge* edge;
};
// Crea un gráfico con vértices V y bordes E
Graph* createGraph(int V, int E)
{
Graph* graph = new Graph();
graph->V = V;
graph->E = E;
graph->edge = new Edge[graph->E *
sizeof(Edge)];
return graph;
}
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
void Union(int parent[], int x, int y)
{
int xset = find(parent, x);
int yset = find(parent, y);
if(xset != yset)
{
parent[xset] = yset;
}
}
// La función principal para comprobar si un gráfico determinado contiene
ciclos o no
int isCycle( Graph* graph )
{
int *parent = new int[graph->V *
sizeof(int)];
memset(parent, -1, sizeof(int) *
graph->V);
// Iterar a través de todos los
bordes del gráfico, encontrar subconjunto de ambos
// vértices de cada borde, si
ambos subconjuntos son iguales, entonces
// hay un ciclo en el
gráfico.
for(int i = 0; i < graph->E; ++i)
{
int x = find(parent,
graph->edge[i].src);
int y = find(parent,
graph->edge[i].dest);
if (x == y) return
1;
Union(parent, x, y);
}
return 0;
}
// Principal
int main()
{
/*Grafo
0
| \
| \
1---2 */
int V = 3, E = 3;
Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if (isCycle(graph))
cout<<" El grafo
contiene ciclo ";
else
cout<<"g El grafo no
contiene ciclo ";
return 0;
}
Salida: El grafo contiene ciclo
6.-
Árbol de expansión mínima *Prim*
Hemos
discutido el algoritmo de Kruskal para el árbol de expansión mínima. Al igual
que el algoritmo de Kruskal, el algoritmo de Prim también es un algoritmo de
Greedy. Comienza con un árbol de expansión vacío. La idea es mantener dos
conjuntos de vértices. El primer conjunto contiene los vértices ya incluidos en
el MST, el otro conjunto contiene los vértices aún no incluidos. En cada paso,
considera todos los bordes que conectan los dos conjuntos, y elige el borde de
mínimo peso de estos bordes. Después de elegir el borde, mueve el otro extremo
del borde al conjunto que contiene la MST.
Un
grupo de bordes que conecta dos conjuntos de vértices en un gráfico se llama
teoría de corte en gráfico. Así, en cada paso del algoritmo de Prim,
encontramos un corte (de dos conjuntos, uno contiene los vértices ya incluidos
en MST y otro contiene el resto de los vértices), escogemos el borde de mínimo
peso del corte e incluimos este vértice al conjunto MST (el conjunto que
contiene los vértices ya incluidos).
¿Cómo
funciona el algoritmo de Prim? La idea detrás del algoritmo de Prim es simple,
un árbol que se extiende significa que todos los vértices deben estar
conectados. Así que los dos subconjuntos disociados (discutidos arriba) de
vértices deben estar conectados para hacer un árbol de expansión. Y deben estar
conectados con el borde de peso mínimo para hacer un árbol de expansión mínimo.
Algoritmo
1)
Crear un conjunto mstSet que lleve la cuenta de los vértices ya incluidos en
MST.
2)
Asignar un valor clave a todos los vértices del gráfico de entrada. Inicializar
todos los valores clave como INFINITO. Asignar el valor de la clave como 0 para
el primer vértice, de modo que sea elegido primero.
3)
Aunque mstSet no incluye todos los vértices
....a)
Escoge un vértice u que no esté en mstSet y que tenga un valor clave mínimo.
....b)
Incluya la u en mstSet.
....c)
Actualiza el valor clave de todos los vértices adyacentes de u. Para actualizar
los valores clave, itera a través de todos los vértices adyacentes. Para cada
vértice adyacente v, si el peso del borde u-v es menor que el valor clave
anterior de v, actualizar el valor clave como peso de u-v
La
idea de usar los valores clave es escoger el borde de peso mínimo del corte.
Los valores clave se utilizan sólo para los vértices que aún no están incluidos
en la MST, el valor clave para estos vértices indica los bordes de peso mínimo
que los conectan al conjunto de vértices incluidos en la MST.
Entendamos
con el siguiente ejemplo:
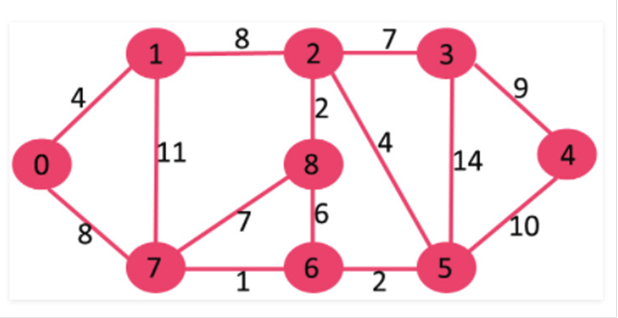
El
conjunto mstSet está inicialmente vacío y las teclas asignadas a los vértices
son {0, INF, INF, INF, INF, INF} donde INF indica infinito. Ahora elige el
vértice con el valor mínimo de la tecla. Se elige el vértice 0, inclúyelo en
mstSet. Así que mstSet se convierte en {0}. Después de incluirlo en mstSet,
actualizar los valores clave de los vértices adyacentes. Los vértices
adyacentes de 0 son 1 y 7. Los valores clave de 1 y 7 se actualizan como 4 y 8.
El siguiente subgráfico muestra los vértices y sus valores clave, sólo se
muestran los vértices con valores clave finitos. Los vértices incluidos en el
MST se muestran en color verde.
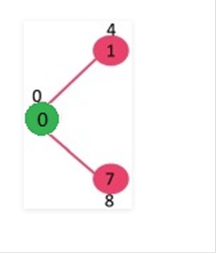
Escoge
el vértice con un valor mínimo de clave y que no esté ya incluido en el MST (no
en el mstSET). El vértice 1 se elige y se añade al mstSet. Así que mstSet ahora
se convierte en {0, 1}. Actualiza los valores clave de los vértices adyacentes
de 1. El valor clave del vértice 2 se convierte en 8.
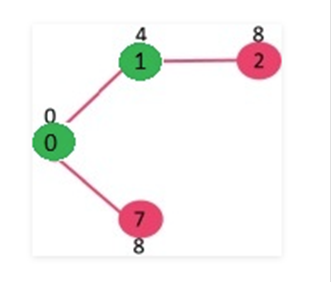
Escoge
el vértice con un valor mínimo de clave y que no esté ya incluido en el MST (no
en el mstSET). Podemos elegir el vértice 7 o el vértice 2, dejando que el
vértice 7 sea elegido. Así que mstSet ahora se convierte en {0, 1, 7}. Actualiza
los valores clave de los vértices adyacentes de 7. El valor clave del vértice 6
y 8 se convierte en finito (1 y 7 respectivamente).
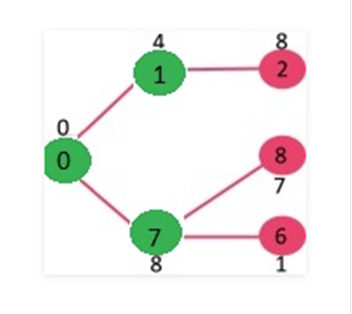
Escoge
el vértice con un valor mínimo de clave y que no esté ya incluido en el MST (no
en el mstSET). Se ha elegido el vértice 6. Así que mstSet ahora se convierte en
{0, 1, 7, 6}. Se actualizan los valores clave de los vértices adyacentes de 6.
Se actualizan los valores clave de los vértices 5 y 8.
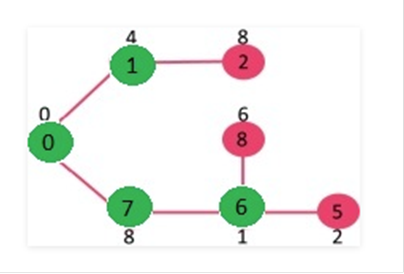
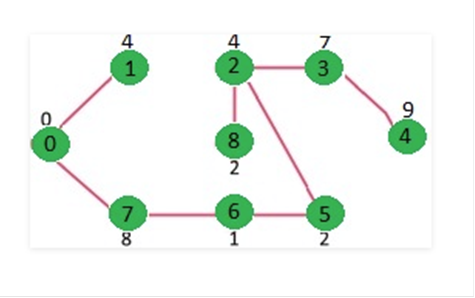
Repetimos
los pasos anteriores hasta que mstSet incluya todos los vértices del gráfico
dado. Finalmente, obtenemos el siguiente gráfico.
¿Cómo
implementar el algoritmo anterior?
Utilizamos
una matriz booleana mstSet[] para representar el conjunto de vértices incluidos
en MST. Si un valor mstSet[v] es verdadero, entonces el vértice v está incluido
en MST, de lo contrario no. La matriz key[] se utiliza para almacenar los
valores clave de todos los vértices. Otra matriz matriz matriz[] para almacenar
índices de los nodos padres en MST. El arreglo padre es el arreglo de salida
que se utiliza para mostrar el MST construido.
#include <bits/stdc++.h>
using namespace std;
//Nº vértices del grafo
#define V 5
// Una función de utilidad para encontrar el vértice con
// valor clave mínimo, del conjunto de vértices
// no incluido aún en el MST
int minKey(int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for (int v = 0; v
< V; v++)
if (mstSet[v] == false
&& key[v] < min)
min
= key[v], min_index = v;
return min_index;
}
// Una función de utilidad para imprimir el
// construido MST almacenado en parent[]
void printMST(int parent[], int graph[V][V])
{
cout<<"Edge \tWeight\n";
for (int i = 1; i < V; i++)
cout<<parent[i]<<"
- "<<i<<" \t"<<graph[i][parent[i]]<<"
\n";
}
// Función para construir e imprimir MST para
// un gráfico representado usando la adyacencia
// representación matricial
void primMST(int graph[V][V])
{
int parent[V];
int key[V];
bool mstSet[V];
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i]
= false;
key[0] = 0;
parent[0] = -1; // First node is always root of MST
for (int count = 0; count < V - 1; count++)
{
int u = minKey(key,
mstSet);
mstSet[u] = true;
// Actualizar el valor clave
y el índice padre de
// los vértices adyacentes
del vértice elegido.
// Considere sólo aquellos
vértices que no son
// ...aún incluido en el
MST...
for (int v = 0; v < V;
v++)
// el gráfico[u][v] no es
cero sólo para los vértices adyacentes de m
// mstSet[v] es falso
para los vértices que aún no están incluidos en el MST
// Actualizar la tecla
sólo si el gráfico[u][v] es más pequeño que la tecla[v]
if
(graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v]
= u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
// Driver code
int main()
{
/* Grafo
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9
*/
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{
2, 0, 3, 8, 5 },
{
0, 3, 0, 0, 7 },
{
6, 8, 0, 0, 9 },
{
0, 5, 7, 9, 0 } };
primMST(graph);
return 0;
}
Salida:
Borde Peso
0 - 1 2
1 - 2 3
0 - 3 6
1 - 4 5
La complejidad temporal del programa anterior es O(V^2). Si el gráfico de entrada
se representa usando la lista de adyacencias, entonces la complejidad de tiempo
del algoritmo de Prim puede reducirse a O(E log V) con la ayuda de la pila
binaria
7.-
Árbol de expansión mínima *Kruskal*
¿Qué
es el árbol de expansión mínima?
Dado
un gráfico conectado y no dirigido, un árbol de expansión de ese gráfico es un
subgrafo que es un árbol y conecta todos los vértices juntos. Un solo gráfico
puede tener muchos árboles de expansión diferentes. Un árbol de expansión
mínima (MST) o árbol de expansión de peso mínimo para un gráfico ponderado,
conectado y no dirigido es un árbol de expansión con un peso menor o igual al
peso de todos los demás árboles de expansión. El peso de un árbol de expansión
es la suma de los pesos dados a cada borde del árbol de expansión.
¿Cuántos
bordes tiene un árbol de expansión mínima?
Un
árbol de mínimo alcance tiene (V - 1) bordes donde V es el número de vértices
en el gráfico dado.
¿Cuáles
son las aplicaciones del árbol de mínima expansión?
Vea
esto para las aplicaciones de MST.
A
continuación están los pasos para encontrar MST usando el algoritmo de Kruskal
1.
Ordena todos los bordes en orden no decreciente de su peso.
2.
2. Escoge el borde más pequeño. 3. Comprueba si forma un ciclo con el árbol de
envergadura formado hasta ahora. Si no se forma un ciclo, incluye este borde.
Si no, deséchelo.
3.
Repita el paso 2 hasta que haya bordes (V-1) en el árbol de expansión.
El
paso 2 utiliza el algoritmo Union-Find para detectar el ciclo. Así que
recomendamos leer el siguiente post como requisito previo.
Algoritmo
Union-Find | Conjunto 1 (Detección de ciclo en un gráfico)
Algoritmo
de unión | Set 2 (unión por compresión de rango y camino)
#include <bits/stdc++.h>
using namespace std;
class Edge
{
public:
int src, dest, weight;
};
class Graph
{
public:
int V, E;
Edge* edge;
};
Graph* createGraph(int V, int E)
{
Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
class subset
{
public:
int parent;
int rank;
};
int find(subset subsets[], int i)
{
if (subsets[i].parent != i)
subsets[i].parent =
find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank <
subsets[yroot].rank)
subsets[xroot].parent =
yroot;
else if (subsets[xroot].rank >
subsets[yroot].rank)
subsets[yroot].parent =
xroot;
else
{
subsets[yroot].parent =
xroot;
subsets[xroot].rank++;
}
}
int myComp(const void* a, const void* b)
{
Edge* a1 = (Edge*)a;
Edge* b1 = (Edge*)b;
return a1->weight > b1->weight;
}
void KruskalMST(Graph* graph)
{
int V = graph->V;
Edge result[V];
int e = 0;
int i = 0;
// Paso 1: Clasificar todos los
bordes en no decreciente
// orden de su peso. Si no se nos
permite
// cambiar el gráfico dado,
podemos crear una copia de
// conjunto de bordes
qsort(graph->edge, graph->E,
sizeof(graph->edge[0]), myComp);
subset *subsets = new subset[( V * sizeof(subset)
)];
for (int v = 0; v < V; ++v)
{
subsets[v].parent =
v;
subsets[v].rank = 0;
}
// El número de bordes a tomar es igual a V-1
while (e < V - 1 && i <
graph->E)
{
Edge next_edge =
graph->edge[i++];
int x = find(subsets,
next_edge.src);
int y = find(subsets,
next_edge.dest);
if (x != y)
{
result[e++]
= next_edge;
Union(subsets,
x, y);
}
}
cout<<"Following are the edges in the
constructed MST\n";
for (i = 0; i < e; ++i)
cout<<result[i].src<<"
-- "<<result[i].dest<<" ==
"<<result[i].weight<<endl;
return;
}
//Principal
int main()
{
/* Grafo
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4
*/
int V = 4; // Vertices
int E = 5; // Bordes
Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
KruskalMST(graph);
return 0;
}
Salida:
A continuación se muestran los bordes en el MST construido
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Complejidad temporal: O(ElogE) u O(ElogV). La clasificación de los bordes
toma O(ELogE) tiempo. Después de la clasificación, iteramos a través de todos
los bordes y aplicamos el algoritmo de unión de hallazgos. Las operaciones de
búsqueda y unión pueden tomar un tiempo O(LogV). Así que la complejidad general
es el tiempo O(ELogE + ELogV). El valor de E puede ser el del atmosfera O(V2),
así que O(LogV) son O(LogE) iguales. Por lo tanto, la complejidad general del
tiempo es O(ElogE) u O(ElogV)
8.-
Clasificación topológica
La
clasificación topológica para el Gráfico Acíclico Dirigido (DAG) es un
ordenamiento lineal de los vértices, de tal manera que para cada uv de borde
dirigido, el vértice u se antepone a la v en el ordenamiento. La clasificación
topológica para un gráfico no es posible si el gráfico no es un DAG.
Por
ejemplo, una clasificación topológica del siguiente gráfico es "5 4 2 3 1
0". Puede haber más de una clasificación topológica para un gráfico. Por
ejemplo, otra clasificación topológica del siguiente gráfico es "4 5 2 3 1
0". El primer vértice en la clasificación topológica es siempre un vértice
con grado 0 (un vértice sin bordes entrantes).
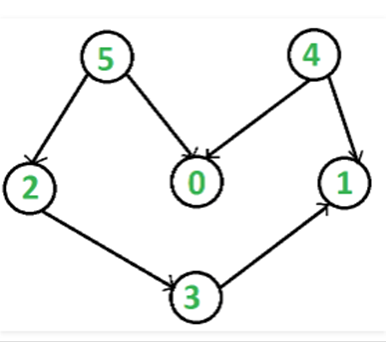
Clasificación
Topológica vs. Profundidad Primera Traversal (DFS):
En
DFS, imprimimos un vértice y luego llamamos recursivamente DFS a sus vértices
adyacentes. En la clasificación topológica, necesitamos imprimir un vértice
antes de sus vértices adyacentes. Por ejemplo, en el gráfico dado, el vértice
"5" debería imprimirse antes del vértice "0", pero a
diferencia de DFS, el vértice "4" también debería imprimirse antes
del vértice "0". Así que la clasificación topológica es diferente de
la DFS. Por ejemplo, una DFS del gráfico mostrado es "5 2 3 1 0 4",
pero no es una clasificación topológica
Algoritmo
para encontrar la clasificación topológica:
Recomendamos
ver primero la implementación del DFS aquí. Podemos modificar la DFS para encontrar
la ordenación topológica de un gráfico. En DFS, partimos de un vértice, primero
lo imprimimos y luego llamamos recursivamente a DFS para sus vértices
adyacentes. En la clasificación topológica, usamos una pila temporal. No
imprimimos el vértice inmediatamente, primero llamamos recursivamente a la
clasificación topológica para todos sus vértices adyacentes, y luego lo
empujamos a una pila. Finalmente, imprimimos el contenido de la pila. Obsérvese
que un vértice se empuja a la pila sólo cuando todos sus vértices adyacentes (y
sus vértices adyacentes y así sucesivamente) ya están apilados.
A
continuación se presentan las implementaciones de la clasificación topológica.
Por favor, vea el código para la primera travesía de profundidad para un
gráfico desconectado y note las diferencias entre el segundo código dado allí y
el código de abajo
#include<iostream>
#include <list>
#include <stack>
using namespace std;
class Graph
{
//vertices
int V;
list<int> *adj;
void topologicalSortUtil(int v, bool visited[],
stack<int> &Stack);
public:
// Constructor
Graph(int V);
void addEdge(int v, int w);
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
// Add w to v’s list.
adj[v].push_back(w);
}
void Graph::topologicalSortUtil(
int v, bool visited[],
stack<int>
&Stack)
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
topologicalSortUtil(*i,
visited, Stack);
Stack.push(v);
}
void Graph::topologicalSort()
{
stack<int> Stack;
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i,
visited, Stack);
while (Stack.empty() == false)
{
cout << Stack.top()
<< " ";
Stack.pop();
}
}
//Principal
int main()
{
// Crea
grafo
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Following is a Topological Sort
of the given graph \n";
g.topologicalSort();
return 0;
}
Salida:
A continuación se muestra una especie de topología del gráfico dado
5 4 2 3 1 0
Análisis de la complejidad:
Complejidad temporal: O(V+E).
El algoritmo anterior es simplemente DFS con una pila extra. Así que la
complejidad de tiempo es la misma que la DFS que es.
Espacio auxiliar: O(V).
El espacio extra es necesario para la pila.
9.-
Encuentra todas las palabras posibles en un tablero de caracteres
Se
le dio un diccionario, un método para hacer búsquedas en el diccionario y un
tablero M x N donde cada celda tiene un carácter. Encontrar todas las palabras
posibles que pueden ser formadas por una secuencia de caracteres adyacentes.
Tenga en cuenta que podemos pasar a cualquiera de los 8 caracteres adyacentes,
pero una palabra no debe tener múltiples instancias de la misma celda.
Ejemplo:
Entrada:
diccionario[] = {"GEEKS", "FOR", "QUIZ",
"GO"};
boggle[][] = {{{'G', 'I', 'Z'},
{\A6}*,
{'Q', 'S', 'E'}};
isWord(str): devuelve verdadero si str
está presente en el diccionario
o bien falso.
Salida: Las siguientes palabras del diccionario están
presentes
GEEKS
PRUEBA
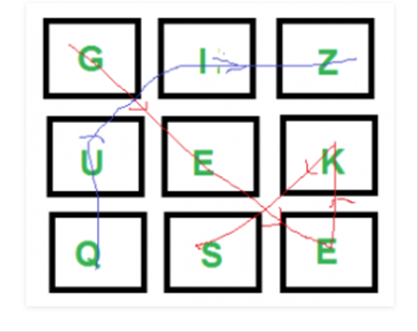
La idea es considerar cada personaje como un
personaje de partida y encontrar todas las palabras que empiecen con él. Todas
las palabras que empiezan con un personaje pueden ser encontradas usando "Profundidad
Primera Travesía". Hacemos la primera travesía de profundidad empezando
por cada célula. Hacemos un seguimiento de las celdas visitadas para
asegurarnos de que una celda se considera sólo una vez en una palabra.
#include <cstring>
#include <iostream>
using namespace std;
#define M 3
#define N 3
string dictionary[] = { "GEEKS", "FOR",
"QUIZ", "GO" };
int n = sizeof(dictionary) / sizeof(dictionary[0]);
// Una función determinada para comprobar si una cadena determinada está
presente en
// diccionario. La implementación es ingenua por simplicidad. Como
// por el diccionario de preguntas se nos da. bool isWord(string& str)
{
// Linearly search all words
for (int i = 0; i < n; i++)
if
(str.compare(dictionary[i]) == 0)
return
true;
return false;
}
void findWordsUtil(char boggle[M][N], bool visited[M][N], int i,
int
j, string& str)
{
visited[i][j] = true;
str = str + boggle[i][j];
if (isWord(str))
cout << str <<
endl;
for (int row = i - 1; row <= i + 1 &&
row < M; row++)
for (int col = j - 1; col
<= j + 1 && col < N; col++)
if
(row >= 0 && col >= 0 && !visited[row][col])
findWordsUtil(boggle,
visited, row, col, str);
str.erase(str.length() - 1);
visited[i][j] = false;
}
void findWords(char boggle[M][N])
{
bool visited[M][N] = { { false } };
string str = "";
// Considera cada personaje y
busca todas las palabras
for (int i = 0; i < M; i++)
for (int j = 0; j < N;
j++)
findWordsUtil(boggle,
visited, i, j, str);
}
// Principal
int main()
{
char boggle[M][N] = { { 'G', 'I', 'Z' },
{
'U', 'E', 'K' },
{
'Q', 'S', 'E' } };
cout << "Following words of dictionary
are present\n";
findWords(boggle);
return 0;
}
10.-
Puentes en un grafo
Un
borde en un gráfico conectado no dirigido es un puente si al quitarlo se
desconecta el gráfico. Para un gráfico no dirigido desconectado, la definición
es similar, un puente es un borde que se quita y que aumenta el número de
componentes desconectados.
Al
igual que los puntos de articulación, los puentes representan las
vulnerabilidades de una red conectada y son útiles para diseñar redes fiables.
Por ejemplo, en una red informática alámbrica, un punto de articulación indica
las computadoras críticas y un puente indica los cables o conexiones críticas.
A
continuación se muestran algunos gráficos de ejemplo con puentes resaltados con
color rojo.
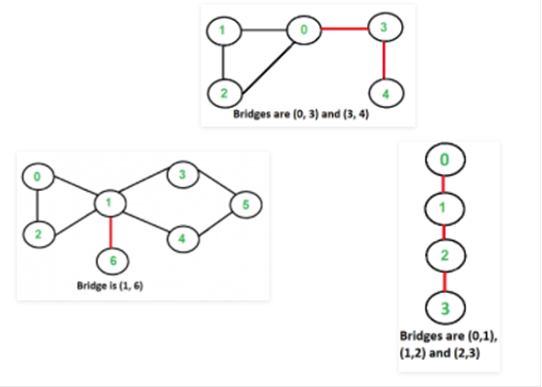
¿Cómo
encontrar todos los puentes en un gráfico dado?
Un
enfoque simple es eliminar uno por uno todos los bordes y ver si la eliminación
de un borde causa un gráfico desconectado. Los siguientes son los pasos del
enfoque simple para el gráfico conectado.
1)
Para cada borde (u, v), haga lo siguiente
.....a)
Quitar (u, v) del gráfico
.....b)
Ver si el gráfico permanece conectado (Podemos usar BFS o DFS)
.....c)
Añade (u, v) de nuevo al gráfico.
La
complejidad temporal del método anterior es O(E*(V+E)) para un gráfico
representado mediante una lista de adyacencias. ¿Podemos hacerlo mejor?
Un
algoritmo O(V+E) para encontrar todos los puentes
La
idea es similar al algoritmo O(V+E) para los puntos de articulación. Hacemos la
DFS transversal del gráfico dado. En el árbol DFS un borde (u, v) (u es el
padre de v en el árbol DFS) es puente si no existe ninguna otra alternativa
para alcanzar u o un ancestro de u desde el subárbol enraizado con v. Como se
ha comentado en el post anterior, el valor low[v] indica el primer vértice
visitado alcanzable desde el subárbol enraizado con v. La condición para que un
borde (u, v) sea puente es, "low[v] > disc[u]".
#include<iostream>
#include <list>
#define NIL -1
using namespace std;
class Graph
{
int V; // vertices
list<int> *adj;
void bridgeUtil(int v, bool visited[], int disc[],
int low[],
int
parent[]);
public:
Graph(int V); // Constructor
void addEdge(int v, int w);
void bridge();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v);
}
void Graph::bridgeUtil(int u, bool visited[], int disc[],
int
low[], int parent[])
{
static int time = 0;
visited[u] = true;
disc[u] = low[u] = ++time;
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
{
int v = *i; // v is
current adjacent of u
if (!visited[v])
{
parent[v]
= u;
bridgeUtil(v,
visited, disc, low, parent);
// Comprueba si el subárbol enraizado con v
tiene un
// conexión con uno de
los ancestros de u
low[u]
= min(low[u], low[v]);
// Si el vértice más bajo
alcanzable desde el subárbol
// bajo v está por debajo
de u en el árbol DFS, luego u-v
// es un puente
if
(low[v] > disc[u])
cout
<< u <<" " << v << endl;
}
else if (v != parent[u])
low[u]
= min(low[u], disc[v]);
}
}
void Graph::bridge()
{
// Mark all the vertices as not visited
bool *visited = new bool[V];
int *disc = new int[V];
int *low = new int[V];
int *parent = new int[V];
// Inicializar las matrices de padres y visitados
for (int i = 0; i < V; i++)
{
parent[i] = NIL;
visited[i] = false;
}
for (int i = 0; i < V; i++)
if (visited[i] == false)
bridgeUtil(i,
visited, disc, low, parent);
}
// Principal
int main()
{
// Crea grafo
cout << "\nBridges in first graph
\n";
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
cout << "\nBridges in second graph
\n";
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.bridge();
cout << "\nBridges in third graph
\n";
Graph g3(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.bridge();
return 0;
}
Salida:
Los puentes en el
primer gráfico
3 4
0 3
Puentes en el
segundo gráfico
2 3
1 2
0 1
Puentes en el tercer
gráfico
1 6
Complejidad
temporal:
La función anterior es simple DFS con arreglos adicionales. Así que la
complejidad temporal es la misma que la DFS que es O(V+E) para la
representación de la lista de adyacencia del gráfico.
&&&&&&&&&&&&&&
&&&&&&&&&
&&&
&