

LOS
10 MEJORES ALGORITMOS NUMÉRICOS
&&&&&&&&&&
&&&&&&&
&&&
&
1.-
Exponenciación modular
Dados
tres números x, y, p, calcula (xy) % p.
Ejemplos :
Entrada:
x = 2, y = 3, p = 5 Salida: 3
Explicación:
2^3 % 5 = 8 % 5 = 3.
Entrada:
x = 2, y = 5, p = 13 Salida: 6
Explicación:
2^5 % 13 = 32 % 13 = 6.
Veamos
las soluciones iterativa y recursiva
Iterativa:
int
power(int x, unsigned int y)
{
int res =
1; // Inicializa
while (y > 0)
{
// Si y es impar,
multiplica x con el resultado
if (y & 1) res = res*x;
y =
y>>1; // y = y/2
x = x*x; //
x^2
}
return res;
El
problema con las soluciones anteriores es que el desbordamiento puede ocurrir
para un gran valor de n o x. Por lo tanto, la potencia se evalúa generalmente
bajo el módulo de un gran número.
A
continuación se muestra la propiedad modular fundamental que se utiliza para
calcular eficientemente la potencia de cálculo en la aritmética modular.
(ab)
mod p = ( (a mod p) (b mod p) ) mod p
Por
ejemplo a = 50, b = 100, p = 13
50
mod 13 = 11
100
mod 13 = 9
(50
* 100) mod 13 = ( (50 mod
13) * (100 mod 13) ) mod 13
o
(5000) mod 13 = ( 11 * 9 ) mod
13
o
8 = 8
A
continuación se muestra la aplicación basada en la propiedad anterior.
Recursiva:
|
#include <iostream> using namespace std;
int power(int
x, unsigned int y, int p) { int
res = 1; // Inicializa x = x % p; //
Actualizar x si es mayor o igual a p if
(x == 0) return 0; while
(y > 0) { //
Si y es impar, multiplica x con el resultado if (y & 1) res = (res*x) % p; y
= y>>1; // y = y/2 x
= (x*x) % p; } return
res; } // Programa principal int main() { int
x = 2; int
y = 5; int
p = 13; cout
<< "El resultado es " << power(x,
y, p); return
0; } |
Salida :
6
La complejidad de
la solución es O(Log y).
2.-
Multiplicación modular inversa
Dados
dos números enteros "a" y "m", encuentre el inverso
multiplicativo modular de "a" bajo el módulo "m".
El
inverso multiplicativo modular es un número entero "x" tal que.
a x ≡ 1 (modulo m)
El
valor de x debe estar en {0, 1, 2, ... m-1}, es decir, en el rango del módulo
entero m.
El
inverso multiplicativo de "un módulo m" existe si y sólo si a y m son
relativamente primos (es decir, si gcd(a, m) = 1).
Ejemplo:
Entrada:
a = 3, m = 11
Salida:
4
Ya
que (4*3) mod 11 = 1, 4 es el módulo inverso de
3(bajo 11).
Uno
podría pensar, 15 también como una salida válida como "(15*3) mod 11"
es
también 1, pero 15 no está en el anillo {0, 1, 2, ... 10}, así que no
válido.
Un
método sencillo es probar todos los números de 1 a m. Por cada número x,
compruebe si (a*x)%m es 1. A continuación se muestra la aplicación de este
método.
#include<iostream>
using namespace
std;
int modInverse(int a, int m)
{
a = a%m;
for (int
x=1; x<m; x++)
if
((a*x) % m == 1)
return x;
}
// Principal
int main()
{
int a = 3, m = 11;
cout << modInverse(a, m);
return 0;
}
Salida: 4
Complejidad temporal: O(m)
3.-
Prueba de Primalidad (Método Fermat)
Si
se le da un número n, compruebe si es primo o no. Hemos introducido y discutido
el método de la Escuela para la prueba de primacía en el Conjunto 1.
Prueba
de Primalidad | Conjunto 1 (Introducción y Método
Escolar)
En
este post, se discute el método de Fermat. Este método es un método
probabilístico y se basa en el pequeño teorema de Fermat.
Teorema
de Fermat:
Si
n es un número primo, entonces por cada a, 1 < a < n-1,
an-1
≡ 1 (mod n)
O
an-1
% n = 1
Ejemplo:
Dado que 5 es primo, 24 ≡ 1 (mod 5) [o 24%5 =
1],
34 ≡ 1 (mod
5) y 44 ≡ 1 (mod 5)
Como el 7 es primo, 26 ≡ 1 (mod 7),
36 ≡ 1 (mod
7), 46 ≡ 1 (mod 7)
56 ≡ 1 (mod
7) y 66 ≡ 1 (mod 7)
Si
un número dado es primo, entonces este método siempre vuelve a ser verdadero.
Si un número dado es compuesto (o no primo), entonces puede devolver verdadero
o falso, pero la probabilidad de producir un resultado incorrecto para el
compuesto es baja y puede reducirse haciendo más iteraciones.
//
El valor más alto de k indica la probabilidad de que sea correcto
//
los resultados de las entradas compuestas se hacen más altos. Para el primer
//
entradas, el resultado es siempre correcto
1)
Repita las siguientes k veces:
a) Elija una al azar en el rango [2, n -
2]
b) Si gcd(a, n)
≠ 1, entonces devuelve falso
c) Si an-1 ≢
1 (mod n), entonces devuelve falso
2)
Retorno verdadero [probablemente primo].
#include <bits/stdc++.h>
using namespace
std;
int power(int a, unsigned int n, int p)
{
int res =
1;
a = a % p;
while (n > 0)
{
if
(n & 1) res = (res*a) % p;
n = n>>1; // n = n/2
a = (a*a) % p;
}
return res;
}
int gcd(int a, int b)
{
if(a < b)
return
gcd(b, a);
else if(a%b == 0)
return
b;
else return
gcd(b, a%b);
}
// Si n es primo, entonces siempre regresa verdadero, Si n es
// compuesto que devuelve falso con alta probabilidad
// Un valor más alto de k aumenta la probabilidad de que sea correcto
resultado
bool isPrime(unsigned int n, int k)
{
if (n <= 1 || n == 4) return false;
if (n <= 3) return true;
while (k>0)
{
// Escoge un número al azar en
[2..n-2]
// En los casos de las
esquinas, asegúrese de que n > 4
int a =
2 + rand()%(n-4);
if (gcd(n, a) != 1)
return false;
if (power(a, n-1, n) != 1)
return false;
k--;
}
return true;
}
// Principal
int main()
{
int k = 3;
isPrime(11, k)? cout << " Verdadero \n": cout << " Falso \n";
isPrime(15, k)? cout << " Verdadero \n": cout << " Falso \n";
return 0;
}
Salida: Verdadero Falso
La
complejidad temporal de esta solución es O(k Log n). Tenga en cuenta que la
función de energía toma O(Log n) tiempo.
Observe
que el método anterior puede fallar incluso si aumentamos el número de
iteraciones (más alto k). Existen algunos números compuestos con la propiedad
de que para cada a < n, gcd(a, n) = 1 y an-1 ≡
1 (mod n). Tales números se llaman números de Carmichael. La prueba de primacía de Fermat se utiliza a
menudo si se necesita un método rápido para el filtrado, por ejemplo en la fase
de generación de claves del algoritmo criptográfico de clave pública RSA.
4.-
La función de Totient de Euler
¿La
función de Euler Totient? (n) para una entrada n es
la cuenta de los números en {1, 2, 3, ..., n} que son relativamente primos a n,
es decir, los números cuyo GCD (Greatest Common Divisor) con n es 1.
Ejemplos
:
?(1)
= 1
gcd(1,
1) es 1
?(2)
= 1
gcd(1,
2) es 1, pero gcd(2, 2) es 2.
?(3)
= 2
gcd(1,
3) es 1 y gcd(2, 3) es 1
?(4)
= 2
gcd(1,
4) es 1 y gcd(3, 4) es 1
?(5)
= 4
gcd(1,
5) es 1, gcd(2, 5) es 1,
gcd(3,
5) es 1 y gcd(4, 5) es 1
?(6)
= 2
gcd(1,
6) es 1 y gcd(5, 6) es 1,
¿Cómo
se computa ?(n) para una entrada n?
Una
solución simple es iterar a través de todos los números del 1 al n-1 y contar
los números con gcd con n como 1. A continuación se
muestra la implementación del método simple para calcular la función Totient de Euler para un entero de entrada n.
#include <iostream>
using namespace
std;
int gcd(int a, int b)
{
if (a == 0) return b;
return gcd(b % a, a);
}
int phi(unsigned int n)
{
unsigned int result = 1;
for (int
i = 2; i < n; i++)
if
(gcd(i, n) == 1)
result++;
return result;
}
// Principal
int main()
{
int n;
for (n = 1; n <= 10;
n++)
cout
<< "phi("<<n<<") = " << phi(n)
<< endl;
return 0;
}
Salida:
phi(1) = 1
phi(2) = 1
phi(3) = 2
phi(4) = 2
phi(5) = 4
phi(6) = 2
phi(7) = 6
phi(8) = 4
phi(9) = 6
phi(10) = 4
El
código anterior llama a la función gcd O(n) veces. La
complejidad temporal de la función gcd es O(h) donde
"h" es el número de dígitos en un número menor de dos números dados.
Por lo tanto, un límite superior en la complejidad temporal de la solución
anterior es O(nLogn)
5.-
La criba de Eratóstenes
Dado
un número n, imprime todos los primos menores o iguales que n. También se da
que n es un número pequeño.
Ejemplo:
Entrada
: n =10
Salida
: 2 3 5 7
Entrada
: n = 20
Salida:
2 3 5 7 11 13 17 19
La
criba de Eratóstenes es una de las formas más eficientes de encontrar todos los
primos más pequeños que n cuando n es menor de 10 millones o similar
Crear
una lista de números enteros consecutivos del 2 al n: (2, 3, 4, …, n).
Inicialmente,
dejemos que p sea igual a 2, el primer número primo.
Empezando
por p2, cuente en incrementos de p y marque cada uno de estos números mayores o
iguales a p2 en la lista. Estos números serán p(p+1), p(p+2), p(p+3), etc..
Encuentra
el primer número mayor que p en la lista que no está marcado. Si no existe tal
número, detente. De lo contrario, dejemos que p sea ahora igual a este número
(que es el siguiente primo), y repita desde el paso 3.
A
continuación se muestra la implementación del algoritmo anterior. En la
siguiente implementación, se utiliza una matriz booleana arr[]
de tamaño n para marcar múltiplos de números primos
#include <bits/stdc++.h>
using namespace
std;
void SieveOfEratosthenes(int n)
{
// Crear una matriz booleana
"prime[0..n]" e inicializar
// todas las entradas son
verdaderas. Un valor en primo[i] será
// finalmente ser falso si no soy
un primo, sino verdadero. bool
prime[n+1];
memset(prime, true, sizeof(prime));
for (int
p=2; p*p<=n; p++)
{
if
(prime[p] == true)
{
// Actualizar todos los múltiplos
de p mayor que o
// igual al cuadrado de
ella
// números que son
múltiplos de p y son
// menos de p^2 ya han
sido marcados.
for (int i=p*p; i<=n; i += p)
prime[i]
= false;
}
}
for (int
p=2; p<=n; p++)
if
(prime[p])
cout << p << " ";
}
// Principal
int main()
{
int n = 30;
cout << " Los
siguientes son los números primos menores "
<< " o
iguales a " << n << endl;
SieveOfEratosthenes(n);
return 0;
}
Salida:
Los siguientes son los números primos menores o iguales a 30
2 3 5 7 11 13 17 19 23 29
Complejidad temporal: O(n*log(log(n))
6.-
Convexidad
Dado un conjunto de puntos en el plano, el casco
convexo del conjunto es el polígono convexo más pequeño que contiene todos los
puntos del mismo.
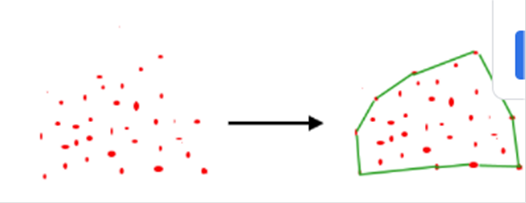
¿Cómo
comprobar si dos segmentos de línea dados se cruzan?
La
idea del Algoritmo de Jarvis es simple, empezamos
desde el punto más a la izquierda (o punto con un valor mínimo de coordenadas
x) y seguimos envolviendo puntos en sentido contrario a las agujas del reloj.
La gran pregunta es, dado un punto p como punto actual, ¿cómo encontrar el
siguiente punto en la salida? La idea es usar la orientación() aquí. El
siguiente punto se selecciona como el punto que supera a todos los demás puntos
en orientación antihoraria, es decir, el siguiente
punto es q si para cualquier otro punto r, tenemos "orientación(p, q, r) =
antihorario". A continuación se presenta el
algoritmo detallado.
1)
Inicializar p como el punto más a la izquierda.
2)
Hacer el seguimiento mientras no volvemos al primer (o más a la izquierda)
punto.
.....a)
El siguiente punto q es el punto tal que el trillizo (p, q, r) es en sentido
contrario a las agujas del reloj para cualquier otro punto r.
.....b)
next[p] = q (Guarda q como el siguiente de p en el
casco convexo de salida).
.....c)
p = q (Poner p como q para la siguiente iteración).
#include <bits/stdc++.h>
using namespace
std;
struct Point
{
int x, y;
};
// Para encontrar la orientación del trillizo ordenado (p, q, r).
// La función devuelve los siguientes valores
// 0 --> p, q y r son colineales
// 1 --> En el sentido de las agujas del reloj
// 2 --> En sentido contrario a las agujas del reloj
int orientation(Point
p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x
- q.x) -
(q.x - p.x) * (r.y
- q.y);
if (val == 0) return 0; // colineal
return (val > 0)? 1:
2;
}
void convexHull(Point
points[], int n)
{
if (n < 3) return;
vector<Point> hull;
int l = 0;
for (int
i = 1; i < n; i++)
if
(points[i].x < points[l].x)
l =
i;
// Empieza desde el punto más a
la izquierda, sigue moviéndote en sentido contrario a las agujas del reloj
// hasta llegar al punto de
partida de nuevo. Este bucle corre O(h)
// veces donde h es el número de
puntos en el resultado o la salida.
int p = l, q;
do
{
hull.push_back(points[p]);
// Buscar un punto 'q' tal
que la orientación(p, x,
// q) es en sentido contrario
a las agujas del reloj para todos los puntos "x". La idea
// ...es llevar un registro
de las últimas visitas a la mayoría de los relojes...
// punto sabio en la q. Si
algún punto 'i' es más contrareloj-
// sabio que q, luego
actualizar q.
q = (p+1)%n;
for
(int i = 0; i < n; i++)
{
if (orientation(points[p], points[i], points[q]) == 2)
q
= i;
}
// Ahora q es el más en
sentido contrario a las agujas del reloj con respecto a p
// Ponga p como q para la
siguiente iteración, para que q se añada a
// resultado 'hull'
p = q;
} while (p !=
l);
for (int
i = 0; i < hull.size(); i++)
cout
<< "(" << hull[i].x <<
", "
<<
hull[i].y << ")\n";
}
// Principal
int main()
{
Point points[] = {{0, 3},
{2, 2}, {1, 1}, {2, 1},
{3,
0}, {0, 0}, {3, 3}};
int n = sizeof(points)/sizeof(points[0]);
convexHull(points, n);
return 0;
}
Salida:
La salida son puntos del casco convexo.
(0, 3)
(0, 0)
(3, 0)
(3, 3)
Complejidad temporal: Para cada punto del casco examinamos todos los demás
puntos para determinar el siguiente punto. La complejidad temporal es ?(m * n)
donde n es el número de puntos de entrada y m es el número de puntos de salida
o del casco (m <= n). En el peor de los casos, la complejidad temporal es
O(n 2). El peor caso ocurre cuando todos los puntos están en el casco (m = n)
7.-
Algoritmos euclidianos básicos y extendidos
El
GCD de dos números es el mayor número que divide a ambos. Una forma sencilla de
encontrar el GCD es factorizar ambos números y
multiplicar los factores comunes.

Algoritmo
euclidiano básico para el GCD
El
algoritmo se basa en los siguientes hechos.
Si
restamos un número menor de un número mayor (reducimos un número mayor), el GCD
no cambia. Así que si seguimos restando repetidamente el mayor de dos,
terminamos con GCD.
Ahora,
en lugar de la resta, si dividimos un número más pequeño, el algoritmo se
detiene cuando encontramos el resto 0.
A
continuación se muestra una función recursiva para evaluar el GCD usando el
algoritmo de Euclides.
#include <bits/stdc++.h>
using namespace
std;
int gcd(int a, int b)
{
if (a == 0)
return
b;
return gcd(b % a, a);
}
// Principal
int main()
{
int a = 10, b = 15;
cout <<
"GCD(" << a << ", "
<< b <<
") = " << gcd(a, b)
<<
endl;
a = 35, b = 10;
cout <<
"GCD(" << a << ", "
<< b <<
") = " << gcd(a, b)
<<
endl;
a = 31, b = 2;
cout <<
"GCD(" << a << ", "
<< b <<
") = " << gcd(a, b)
<<
endl;
return 0;
}
Salida:
GCD(10, 15) = 5
GCD(35, 10) = 5
GCD(31, 2) = 1
Complejidad temporal: O(Log min(a, b))
8.-
Criba segmentada
Dado
un número n, imprime todos los primos menores que n. Por ejemplo, si el número
dado es 10, salida 2, 3, 5, 7.
Un
enfoque sencillo es ejecutar un bucle de 0 a n-1 y comprobar que cada número
tiene primacía. Un mejor enfoque es usar la Criba de Eratóstenes.
void simpleSieve(int limit)
{
// Crear una matriz booleana
"mark[0..limit-1]" y
// Inicializar todas las entradas
como verdaderas. Un valor
// en mark[p]
será finalmente falso si 'p' no es
// un primo, si no es cierto.
bool mark[limit];
memset(mark, true, sizeof(mark));
// Uno por uno atraviesa todos
los números para que su
// los múltiplos pueden ser
marcados como compuestos.
for (int
p=2; p*p<limit; p++)
{
if
(mark[p] == true)
{
for (int i=p*p; i<limit; i+=p)
mark[i] = false;
}
}
for (int
p=2; p<limit; p++)
if
(mark[p] == true)
cout << p << " ";
}
9.-
Teorema del resto chino
Se
nos dan dos matrices num[0..k-1] y rem[0..k-1]. En num[0..k-1], cada par es coprime
(gcd para cada par es 1). Necesitamos encontrar el
mínimo número positivo x de tal manera que:
x % num[0] =
rem[0],
x % num[1] =
rem[1],
.......................
x % num[k-1] =
rem[k-1]
Básicamente,
se nos dan números k que son coprimos por pares, y se
nos dan restos de estos números cuando un número desconocido x es dividido por
ellos. Tenemos que encontrar el mínimo valor posible de x que produce residuos
dados.
Ejemplo:
Entrada:
num[] = {5, 7}, rem[] = {1, 3}
Salida:
31
Explicación:
31
es el número más pequeño tal que:
(1) Cuando lo dividimos por 5, obtenemos el
resto 1.
(2) Cuando lo dividimos por 7, obtenemos el
resto 3.
Que
num[0], num[1], ...num[k-1] sean números enteros positivos que se copriman por pares. Entonces, para cualquier secuencia dada
de números enteros rem[0], rem[1], ... rem[k-1], existe un número entero x que
resuelve el siguiente sistema de congruencias simultáneas.
La
primera parte es clara en cuanto a la existencia de una x. La segunda parte
establece básicamente que todas las soluciones (incluyendo la mínima) producen
el mismo resto cuando se dividen por el subproducto de n[0], num[1], .. num[k-1]. En el
ejemplo anterior, el producto es 3*4*5 = 60. Y 11 es una solución, otras
soluciones son 71, 131, .. etc. Todas estas soluciones producen el mismo resto
cuando se dividen por 60, es decir, son de la forma 11 + m*60 donde m >= 0.
Una
aproximación sencilla para encontrar x es comenzar con 1 y aumentarlo de a uno
y comprobar si dividiéndolo con los elementos dados en num[]
produce los correspondientes restos en rem[]. Una vez que encontramos tal x, la
devolvemos.
#include<bits/stdc++.h>
using namespace
std;
// k es el tamaño de num[] y rem[]. Devuelve el más pequeño
// número x tal que:
// x % num[0] = rem[0],
// x % num[1] = rem[1],
// ..................
// x % num[k-2] = rem[k-1]
// Asunción: Los números en num[] son coprime a pares
// (gcd por cada par es 1)
int findMinX(int num[], int
rem[], int k)
{
int x = 1; // Initialize result
while (true)
{
int
j;
for
(j=0; j<k; j++ )
if (x%num[j] != rem[j])
break;
if
(j == k) return x;
x++;
}
return x;
}
// Principal
int main(void)
{
int num[]
= {3, 4, 5};
int rem[] = {2, 3, 1};
int k = sizeof(num)/sizeof(num[0]);
cout << "x is " << findMinX(num, rem, k);
return 0;
}
Salida: x es 11
10.-
Teorema de Lucas
Dados
tres números n, r y p, calcular el valor de Cr,n mod p.
Ejemplo:
Entrada:
n = 10, r = 2, p = 13
Salida:
6
Explicación:
C2,10 es 45 y 45 % 13 es 6.
Hemos
introducido el problema de desbordamiento y discutido la solución basada en la
Programación Dinámica en el set 1 anterior. La complejidad temporal de la
solución basada en la programación dinámica es O(n*r) y requiere O(n) espacio.
El tiempo y el espacio extra se vuelven muy altos para los grandes valores de
n, especialmente los valores cercanos a 109.
#include<bits/stdc++.h>
using namespace
std;
int nCrModpDP(int n, int r, int
p)
{
int C[r+1];
memset(C, 0, sizeof(C));
C[0] = 1;
for (int
i = 1; i <= n; i++)
{
for
(int j = min(i, r); j > 0; j--)
C[j] = (C[j] + C[j-1])%p;
}
return C[r];
}
// Función basada en el Teorema de Lucas que devuelve nCr
% p
// Esta función funciona como la conversión de decimal a binario
// función recursiva. Primero
calculamos los últimos dígitos de
// n y r en la base p, luego se repiten para los dígitos restantes
int nCrModpLucas(int n, int r, int
p)
{
if (r==0) return 1;
int ni = n%p,
ri = r%p;
// Calcular el resultado de los
últimos dígitos calculados arriba, y
// para los dígitos
restantes. Multiplique los dos
resultados y
// calcular el resultado de la
multiplicación en el módulo p.
return (nCrModpLucas(n/p,
r/p, p) * // Last digits of
n and r
nCrModpDP(ni, ri, p)) % p;
// Remaining digits
}
// Principal
int main()
{
int n = 1000, r = 900, p
= 13;
cout << "Value of nCr % p is " << nCrModpLucas(n,
r, p);
return 0;
}
Salida:
El valor de Cr,n % p es 8
Complejidad temporal: La complejidad temporal de esta solución es O(p2 * Logp n). Hay dígitos O(Logp n) en
la representación de la base p de n. Cada uno de estos dígitos es más pequeño
que p, por lo tanto, los cálculos para los dígitos individuales toman O(p2).
Nótese que estos cálculos se hacen usando el método DP que toma O(n*r) tiempo.
&&&&&&&&&&
&&&&&&&
&&&
&