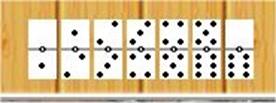
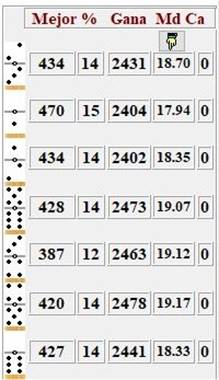
Figura 1

En el muy equilibrado reparto que presentamos y con 3000 pruebas observamos que las mejores fichas de salida son el [5-4] y el [4-3] pero a muy escasa distancia entre ellas e incluso con el resto de las opciones, debido a la igualdad en todos los aspectos que representa el reparto.

Pero cuestión diferentes es la siguiente: Sí con cualquier reparto conocemos todas las fichas del resto de los jugadores : ¿Podremos calcular cuál será la mejor salida, cual es la secuencia de fichas que se jugarán, quien ganará la mano y con qué valor o total de tantos?

No parecería ser tan difícil al tener todo el juego descubierto, ya que jugadores avezados insisten en conocer la ubicación de fichas, indicando que con ella podrían “calcular” el juego a seguir ¿será cierto esto y hasta qué punto puede lograrse?

Todos los ejercicios deben realizarse sin ver la solución final, por supuesto.

Lo intentaremos con el reparto anterior pero conociendo todas las fichas del resto de los jugadores:

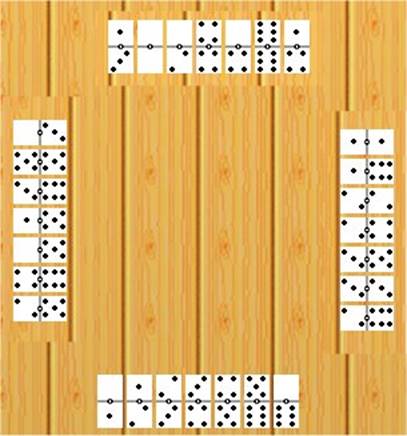
Figura 2

1) ¿Qué ficha es la mejor salida?: [0-6]

2) ¿Qué secuencia de fichas dan el mejor valor posible?:

(S:1) [0--6] (E:2) [1--6] (N:3) [0--0] (O:4) [0--3] (S:1) [3--4] (E:2) [2--4] (N:3) [0--2] (O:4) [1--5] (S:1) [5--6] (E:2) [2--6] (N:3) [0--4] (O:4) [2--5] (S:1) [4--5] (E:2) [Pas] (N:3) [1--4] (O:4) [4--6] (S:1) [1--2] (E:2) [2--2] (N:3) [6--6] (O:4) [3--6] (S:1) [2--3]

3) ¿Qué pareja gana la mano?: N-S

4) ¿Cuántos tantos obtienen los ganadores en la mano?: 44

¿Alguien puede calcular esto y además con tiempo limitado? Es posible que con tantos “expertos” alguno lo haga pero me gustaría saber quién y que lo demostrase en vivo, pero no creo que aceptase el reto. ¿por qué será?

Hacer notar que en este caso concreto la que es mejor salida a priori. [5-4], ¡pierde la mano con 92 tantos en contra! ¿Alguien puede calcular, viendo todas las fichas como es el caso, la secuencia de salir por él [5-4]? Va a ser que no así que la reflejaremos:

(S:1) [4--5 (E:2) [2--4] (N:3) [0--2 (O:4) [0--5] (S:1) [5--6] (E:2) [2--6] (N:3) [Pas] (O:4) [2--5] (S:1) [Pas] (E:2) [3--5] (N:3) [1--3] (O:4) [1--5] (S:1) [Pas] (E:2) [Pas] (N:3) [Pas] (O:4) [5--5]

Avanzamos cuatro puestas, por ejemplo: (S:1)[5-4] (E:2)[4-2] (N:3)[2-0], (O:4) [5-5]:

1) ¿Qué ficha es la mejor entre las del jugador en turno (S:1)?: [0-6]

2) ¿Qué secuencia de fichas dan el mejor valor posible?:

(S:1) [0--6] (E:2) [1--6] (N:3) [1--4] (O:4) [4--6] (S:1) [5--6] (E:2) [2--6] (N:3) [6--6] (O:4) [2--5] (S:1) [Pas] (E:2) [3--5] (N:3) [1--3] (O:4) [1--5] (S:1) [Pas] (E:2) [Pas] (N:3) [Pas] (O:4) [3--6] (S:1) [2--3] (E:2) [2--2] (N:3) [Pas] (O:4) [0--5] (S:1) [1--2] (E:2) [1--1] (N:3) [0--4] (O:4) [Pas] (S:1) [3--4]

(E:2) [3--3]

3) ¿Qué pareja gana la mano?: E-O

4) ¿Cuántos tantos obtienen los ganadores en la mano?: 12

Podríamos seguir hasta la misma culminación de mano completa aunque el objetivo de la muestra de dificultad ya se hace patente en el caso visto.

Seguiremos con otros ejercicios y ejemplos.

joseluis.gonzalez@realidad-simulada.es

Todos los derechos reservados son propiedad legal e intelectual exclusiva y registrada a nombre de

José Luis González Sanz

realidad-simulada.es